第一章 数据库的存储结构
1.1文件组织结构
1.1.1文件分页
DBMS中可以看到数据库是以文件的形式存储在磁盘中的,对目前大部分数据库来说都是将数据存储于磁盘上,对于这类存储介质来说,因为其是非易失性存储,这意味着对于系统而言他的寻址方式是块寻址的,必须先将包含这个值的一个块的数据加载到内存中(目前也有基于NVEM存储开发的数据库)。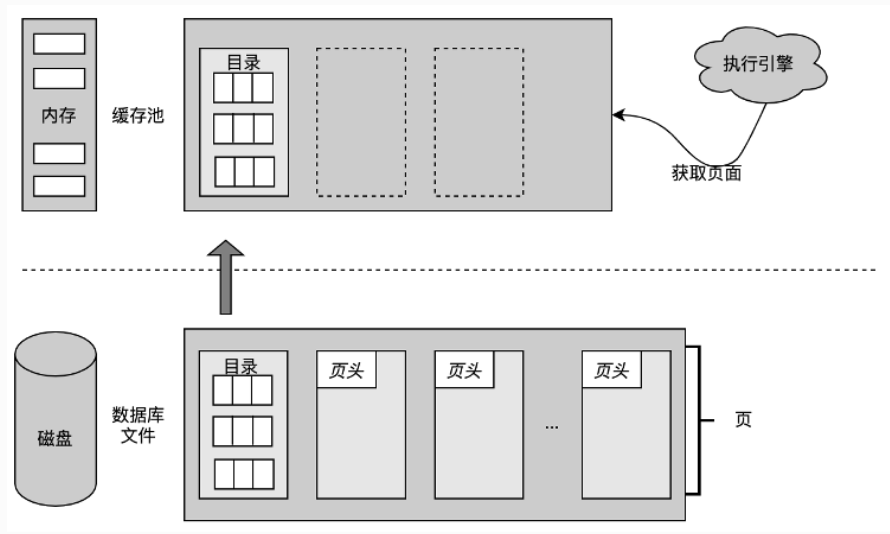
主流操作系统提供的通常为无结构的流文件,DBMS会将每个文件再划分为固定大小的数据块,称为页(page)。页是DBMS在磁盘和内存间交换数据的基本单元。如果需要对数据库进行读写操作,DBMS需要先将数据从磁盘读取到内存中的缓冲池内,缓冲池管理器负责在磁盘和内存之间以页为单位进行数据交换。DBMS的执行引擎在语句处理过程中需要使用某个数据页时,会向缓冲池提出请求,缓冲池管理器负责将该页读入内存,并向执行引擎提供该页在内存中的指针。当执行引擎操作那部分内存时,缓冲池管理器必须确保该页面始终驻留在那片内存区域中。
从操作系统的角度来看,一个文件就是一个字节流序列,操作系统并不关心和了解文件的内容以及文件之间的关联性。数据库文件的内容只有创建它的DBMS才知道如何解读,因为它是由DBMS以其特定的方式来组织的。数据库文件的组织和管理由DBMS的存储管理器负责,它将文件划分为页面的集合,并且负责跟踪记录这些页面的使用情况,包括哪些页面存储了什么数据,哪些页面是空闲的等等。页面中可以存储不同类型的数据,比如记录、索引等,但是DBMS通常不会将不同类型的数据混合存储在同一个页面中。
1.1.2页
每个页面都有唯一的标识符,对于DBMS来说,页因为是对于操作系统存在的抽象层,因此页实际是作为一个间接层提供给DBMS,将对应的页面标识符ID映射成文件路径以及偏移量。
系统上层模块请求一个页面时,先给出页面ID,存储管理器将该页面ID转换为文件路径和偏移量,并由此定位到对应页面。
需要注意区分以下两个关于页的概念:
- 硬件页: 即磁盘块,大小通常为4 KB,是磁盘I/O的基本单位。
- 数据库页: 大小通常为磁盘块大小的整数倍,是DBMS在磁盘和缓冲池之间交换数据的基本单位。
二者的区别在于,对硬件页的写操作是原子的,但是对数据库页的写操作则不一定。换言之,如果硬件页的大小为4KB,那么当系统尝试向磁盘写入一个硬件页时,这4KB数据要么全部写入,要么全部不写入,这一点是由存储设备来保证的。
但是,如果数据库页大于硬件页,那么DBMS对一个数据库页的写操作将被操作系统分解为对多个硬件页的写操作,此时DBMS必须采取额外措施来确保数据被安全地写入磁盘,因为系统可能会在将一个数据库页写入到磁盘的过程中发生崩溃,从而导致该数据库页的内容出现不一致性错误。
1.1.2.1 OS中的页
由于系统中的物理内存是随分配不断在变化的,有时候这个程序使用,有时候那个程序在使用。如果不使用逻辑地址直接使用物理地址,那当前进程操作的地址被占用,则不能使用内存。通过将连续的逻辑地址映射成不连续的物理地址,程序将只用关系的连续的逻辑地址,而物理地址再通过一些方法找到并映射过去。
将程序的逻辑地址空间分为若干等大的页,称为 页/页面/虚页 。同样将物理内存分成若干项大小同虚页大小的页,称为 块/页帧/实页。虚页是连续的,实页是不连续的,页表就维护了虚页到实页的映射关系,页表中每一项称为页表项(PTE),表示一个虚页到实页是映射关系。每个进程都有自己的页表,称为进程页表。
程序中使用的虚地址大致如下:
|页号|页内偏移|页表中的内容大致如下(当然还可以有一些标志信息,如是否有读写权限、是否可用等):
页号1: |标记|物理页号|
页号2: |标记|物理页号|
页号3: |标记|物理页号|
页号4: |标记|物理页号|
标注页号仅表示页表项之间的位置关系(连续),不占用实际内存每个进程为了找到自己的进程页表还需要 页表基地址寄存器(PTBR) 的帮忙,其指向进程页表的实页号/页表起始地址(PPN)。进程切换时会切换PTBR的值。
注意 ,页号表示页表项之间的位置关系(连续),实际不占物理内存,通过PTBR+页号x页表项大小算出目标地址
由虚地址到实际物理地址的变化叫做内存映射,过程如下:
┌────┐ ┌────────┬─────────┐
│PTBR│ │虚拟页号│ 页内偏移│ 主存
└─┬──┘ └──┬─────┴────┬────┘ ┌─────────────┐
│ │ │ │ │
│ │ │ │ │
│ │ │ │ │
│ │ │ ├─────────────┤
└──────────+──────────┼────────────►│ │
│ 物理页号 │page table │
x─◄───────────┤ │
│ ├─────────────┤
│ │ │
│ │ │
│ │ │
│ 物理地址 │ │
└───────────► │ │
│ │
│ │
└─────────────┘如果对应地址缺页,则会触发缺页中断。进入内核态(异常/中断型),从磁盘换入或加载内存并填写到内存中,并填写帧号,然后重新进行寻址过程。
如0x000011a3的地址映射过程
- 逻辑地址32位=20位页号+12位页内偏移
- 页表项32位=20位块号(与20位页号对应)+12位标记位
- 物理地址=20位块号+12为页内偏移
页表如下:
起址:PTBR
| +页号 | 标记 | 帧号 |
| ------------ | ---- |
| +0x00001 -> | | 0x000f3 |第一次访问内存,通过PTBR+0x00001找到对应的页表项的地址,读取物理页号/页帧/实页号。再通过帧号0x000f3拼接页内偏移0x1a3得到物理地址(不需要加法,一部分高位,一部分低位,直接拼接更快),第二次访问内存读取数据。至少需要两次内存访问
1.1.2.2 分页机制的优化
要真正获取一个内存中的内容实际需要加载两次内存,第一次是查页表找到物理页号,第一次是根据物理页号加页内偏移到对应内存,因此可以进行时间上的优化。而每个进程都需要维护一个页表,页表本身也是占内存空间的,因此还可以进行空间优化。
1.1.2.3 空间优化与多级页表
引入多级页表有两个原因
- 如果页表大小超过了一个页面的大小/容量,则可能将数据存放到两个不同的页面,将无法通过PTBR+页号的方式找到
- 如通常一个页4KB,32位系统中一PTE有32位4B,故PTE数不应超过1k
- 进程页表本身也是在内存中的,需要占用内存空间
如果不考虑页面容量问题,假设一个页能容纳所有页表项。一个32位的系统和程序,如果页内偏移12位,要访问全部4G内存则需要2^20个物理块/物理页面/物理页号,对应就有2^20个页号/虚页号,即2^20个页表项:
|12位标记位|20位表示物理页号|这么一个页表项32bit=4B,则维护一个进程的页表需要占用2^20x4B=4MB的内存空间。4MB看起来很小,但是操作系统是要运行很多程序的。
如果使用多级页表,应当页表大小==页面容量 ,如将32位分为10位,10位,12位的分级方式。为何10位?10位能索引2^10个PTE,而每个PTE占4B,一个页表刚好就4KB,与页容量相同。如果小于页容量会产生内碎片,浪费;如果大于页容量则无法通过页表起址+offset寻址。
64位系统中则常用9位索引页表,64bit=8B,8Bx2^9=4KB,也刚好是一个页的大小。
虚地址:
| VPN[1] | VPN[0] | 页内偏移 |
PTE:
| PPN[1] | PPN[0] | 页内偏移 |PTBR指向一级页表起始地址,加上VPN[1]可以索引到对应页表项,一级页表中的PPN[1]PPN[0]就是二级页表的起始地址,再通过VPN[0]索引二级也被即可得到物理页号,加上页内偏移得到物理地址。
┌────┐ ┌──────┬─────┬───────┐
│PTBR│ │ VPN1 │VPN0 │offset │
└─┬──┘ └──┬───┴──┬──┴───┬───┘ ┌─────────────┐
│ │ │ │ │ │
│ │ │ │ ├─────────────┤
└─────────x──────┼──────┼──────────────────►│xxxxxxxxxxxxx│
│ │ │x L0 xx│
│ │ PPN1,PPN0 │x xx│
x──────┼─────◄─────────────┤xxxxxxxxxxxxx│
│ │ ├─────────────┤
│ │ │ │
│ │ │ │
│ │ │ │
│ │ ├─────────────┤
└──────┼──────────────────►│xxxxxxxxxxxxx│
│ │x L1 xxx│
│ PPN1,PPN0 │x xxx│
x─────◄─────────────┤xxxxxxxxxxxxx│
│ ├─────────────┤
│ │ │
│ │ │
│ │ │
│ │ │
│ │ │
└──────────────────►│ │
│ │
│ │
│ │
│ │
│ │
└─────────────┘如果发现第一级只有3项指向第二级,而第二级页表有2^10项,所以一共3个页表需要(2^10+3x2^10)x4B = 16KB的内存空间。当然上限还是2^10x2^10个表项x4B占4M空间。问题就是内存的访问次数增加了,前面使用多级页表的方式虽然减少了空间占用,但是内存的访问次数增加了。
1.1.2.4TLB
将最常访问的几个(一般8-128个左右)页表项储存到访问速度更快的硬件中,如关联存储器(相当于哈希表),这个小表的名称为TLB (Translation Lookaside Buffer) 或 快表 。寻址会同时寻找TLB和页表,如果TLB命中则查页表寻址的操作作废。
1.1.2.5使用大页
依旧上述多级页表的例子,但是使用某种机制让大页表地址连续,那么就可以使用起址+offset的方式寻址,而不需要多级页表多次访问内存。
虚地址:
| VPN[1] | VPN[0] | 页内偏移 |
PTE:
| PPN[1] | PPN[0] | 页内偏移 |只是访问一级页表(L0)时其返回PPN[1]作为大页的索引(高10位),然后使用虚拟地址的<VPN[0],页内偏移>所谓大页的页内偏移。如此一来访问次数就降低了。
┌────┐ ┌──────┬─────┬───────┐
│PTBR│ │ VPN1 │VPN0 │offset │
└─┬──┘ └──┬───┴──┬──┴──┬────┘
│ │ │ │
│ │ └──┬──┘ ┌─────────────┐
│ │ │ │ │
│ │ │ ├─────────────┤
└───────x─────────┼───────────►│xxxxxxxxxxxxx│
│ │x L0 xx│
│ PPN1, │x xx│
x───────◄────┤xxxxxxxxxxxxx│
│ ├─────────────┤
│ │ │
│ │ │
│ │ │
│ ├─────────────┤
└───────────►│ │
│ huge page │
│ │
│ │
│ │
│ │
│ │
│ │
├─────────────┤
└─────────────┘1.1.3堆文件
关系型数据库存储的是关系,关系则是记录的集合,这些记录在数据库中有许多组织形式:
- 堆文件组织( heap file organization) :堆文件是页的无序集合,记录在页中以随机的顺序存储。即,一条记录可以放在文件中的任何地方,只要那里有足够的空间存放这条记录,记录间不用考虑先后顺序的。 通常每个关系使用一个单独的堆文件。
- 顺序文件组织(sequential file organization):记录根据其”查找键”的值顺序存储。
- 散列文件组织( hash file organization) :在每条记录的某个或某些属性上计算一个散列函数,根据散列的结果来确定将记录放到文件的哪个页面中。
对于堆存储方式而言,由于这种存储形式对程序员而言是可见的,也就是说可以控制记录的存储。同时这种存储方式不关心记录间存储的顺序,只需要维护堆文件中哪些页面是存储了数据(数据页),哪些是空闲的即可。常见的有两种存储方式:
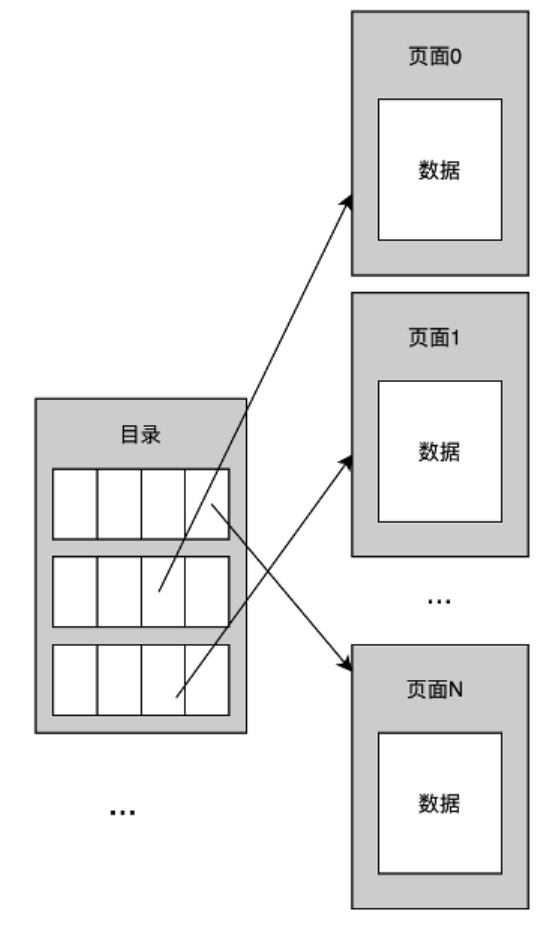
- 链表:以链表的形式将文件中的空闲页和数据页分别勾连起来,并在文件的首页维护两个指针,分别指向空闲页链表和数据页链表的第一个页面。这种方式下,如果想要找到一个特定的数据页,需要从链首开始逐个扫描链表中的页面,直到找到为止,I/O开销较大。

- 页目录:维护一种特殊的页面(目录页),在该页中记录每个数据页的位置以及该数据页中剩余的空闲空间大小。页目录将页面的状态信息集中存放在一起,可以提高查找特定页面的速度。
1.1.4块的存储结构
块在存储中的组织与记录类似,可以简单地看成是由 header + data 数据组成,例如一个块要管理内部所有的记录,需要在块的 header 中保存每个记录的偏移、块最后修改的时间戳、块在存储结构中的位置信息等,因此 header 中的元数据主要是为了方便自身的管理和维护。
下面我们来看一个块里面是如何存放数据的,这里需要强调的是,块里面存储的地址偏移是相对于虚拟地址的偏移,并非实际物理磁盘的偏移。还需要注意,新插入的记录,是从块的末端往中间增长的,而未使用的空间是从 header 之后往块的末端增长的。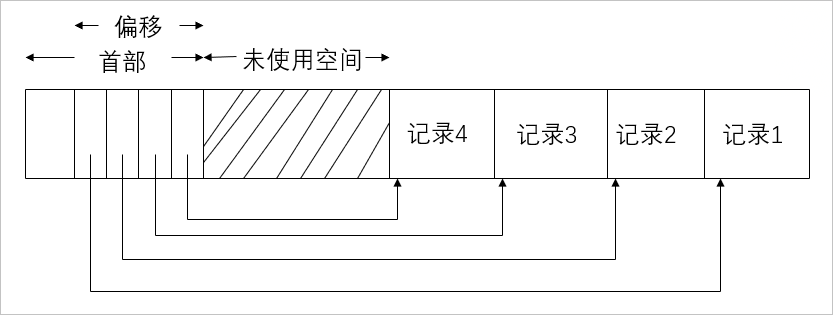
从图中可以看出记录 1 在最后,记录 4 在最前面,因为记录有可能不等长,无法事先根据记录的长度和块的总长来计算好能插入多少数据。
示例:假如一个块的大小是 100。
- 如果记录都等长,都为 10,那么我们可以算出一个块最多能插入 10 条记录,并且可以从块的起始到末端的方向插入,最后刚好到 100 不会报错。
- 如果记录不等长,事先也不知道这个块最多能容纳多少条记录的,如一条长度 10,一条长度 50 的记录,从起始往末端方向编排,如果下一条记录的长度为 50 ,因为不知道块中还有多少空间,也不会提前报错,那必然会插入失败。
但是如果记录是从块的末端往前增长,那在插入 10 和 50 这两条记录后,由于长度为 50 的那条记录的偏移是 40(100 - 10 - 50 = 40),那就能知道当前的空间只剩 40 了,没办法容纳新的记录,然后提前报错然后重新分配块。
1.2页的组织结构
页面的内部结构可以粗分为两个部分:
- 页头 :页头登记了关于页面内容的元数据,如页面大小、校验和、DBMS版本、事务可见性、压缩信息等。有些系统(如Oracle)要求页面是自包含的,即关于该页的所有描述信息都可以在该页面中找到。
- 数据区 :存放数据的区域。这里我们只讨论如何在数据区中存放记录。目前DBMS中最常用的方法是采用槽式页面。这种方法将数据区划分为一个个插槽(slot),每个插槽中放置一条记录。
1.2.1槽式页面
顾名思义,就像一个个slot一样,将记录数据存储到磁盘上,对于这种存储方式而言,需要管理当前页面存储的信息,如最基本的存储记录条数与可用位置,因此需要在页头的位置维护下面信息:- 本页中已使用的槽的数量;
- 最后一个已使用的槽的起始位置;
- 一个槽数组,登记本页中每个记录的起始位置。
并且对于存储的数据库来说,记录数量应该是变长的,也就是说一个页面所存储的记录数量是不确定的,因此槽数组的最大长度是不能决定的,也就是说页头所占的区域大小是不确定的。因此比较合理的做法是,向页中插入记录时,槽数组从前向后增长,而被插入的记录数据则是从页尾向前增长。当槽数组和记录数据相遇时,则认为该页面是满页。
1.2.2插入记录
向关系中插入一条记录时,对于堆文件,只需要找到一个有足够空闲空间能放得下这条记录的页面,或当所有已分配页面中都没有足够空闲空间时,就申请一个新的空闲页,然后将记录放置在那里。
1.2.3删除记录
从页中删除记录时,需要考虑如何回收该记录的空间。一种方法是在页内滑动记录,使得记录间没有空隙,从而保证页面中未使用的区域一定位于槽数组和已使用区域之间。
如果不滑动记录,则需要在页头维护一个空闲区列表,以保证当向页中插入一条新记录时能知道该页中的空闲区在哪里,有多大。而页头通常不必存储全部空闲区列表,只存列表的链头就够了,然后可以使用空闲区自身的空间存储下一个空闲区的信息。
1.2.4修改记录
如果修改的是定长记录,对页面存储没有影响,因为修改后记录占用的空间与修改前完全相同。但是如果修改的是变长记录,就会碰到与插入和删除类似的问题。
如果修改后的记录比其旧版本长,则需要在当前页面中获得更多的空间,这个过程可能涉及记录的滑动。如果当前页面中的空闲区域不够,还需要将记录移动到其他页面。反之,如果记录由于修改而变短可以像删除记录时那样回收其释放的空间。
1.3记录的组织形式
记录本质上就是一个字节序列,如何将这些字节解释为属性类型和值是DBMS的工作。与页面结构类似,记录内部结构也可以分为两部分:
- 记录头 :存放关于记录的元数据,例如DBMS并发控制协议的可见性信息(即哪个事务创建/修改了此记录的信息)、NULL值的位映射等。注意,关于数据库模式的元数据没有必要存储在记录头里。
- 记录数据 :包含记录中各个属性的实际数值。如前所述,大多数DBMS不允许记录的长度超过页面的大小,且一个页面中一般只存放同一个关系的记录。
1.3.1定长记录
定长记录全部由定长字段组成,是最简单的记录组织形式。定长记录的插入和删除是比较容易实现的,因为被删除的记录留出的可用空间恰好是插入新的记录所需要的空间。
定长记录在组织时需要注意的一个问题是内存对齐问题。很多处理器需要在数据的开始地址为4或8的倍数时才能实现更高效的内存读写,所以DBMS在组织记录数据时通常会根据情况使所有字段的起始地址是4或8的倍数。采用这种做法时,一个字段前可能会存在一些没有被上一个字段使用的空间,这些空间其实是被浪费掉了。但尽管如此,这样做还是有必要的。因为记录虽然是存放在磁盘而不是内存中,但是对记录的操作仍需在内存中进行,所以在组织记录时需要考虑如何让它在内存能够被高效访问。
1.3.2变长记录
变长记录允许记录中存在一个或多个变长字段。由于变长字段在记录中的偏移位置是不确定的,因此记录中必须包含足够多的信息,让我们能够方便地提取记录的任何字段。变长记录的实现可以采用以下两种方法。
一种简单有效的实现方法,是将所有定长字段放在变长字段之前,然后在记录头写入以下信息:(1)记录长度;(2)除第一个变长字段之外的所有变长字段的偏移位置。之所以不需要存第一个变长字段的偏移位置,是因为我们知道第一个变长字段就紧跟在定长字段之后。一个变长记录的例子如图所示,该记录共包含四个字段,其中有两个变长字段:name和address。
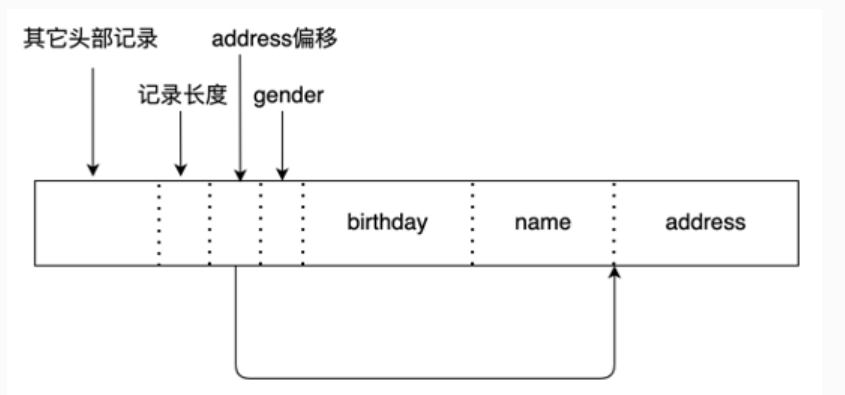
变长记录的另一种表示方法是保持记录定长,将变长部分放在另一个溢出页中,而在记录本身存储指向每一个变长字段开始位置的指针。
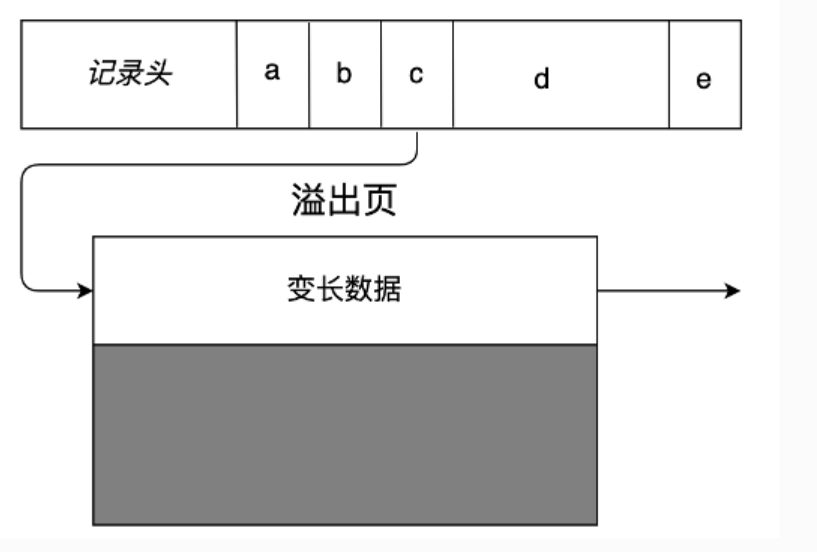
这种做法可以保持记录定长,能够更有效地对记录进行搜索,记录也很容易在页内或页间移动。但是另一方面,将变长部分存储在另一个页中,增加了为检索一条记录的全部数据而需要进行的磁盘I/O次数(损失性能)。
溢出页不仅可以存储变长字段,还可以用于存储大值数据类型的字段,比如TEXT和BLOB字段,这些数据往往需要使用多个页面来存储。
有时候变长记录是由具有可变格式的记录导致的,也就是是字段没有固定格式的记录,在数据库的维度来说是指没有具体表结构的数据,是非结构化的数据,例如 XML 文件。
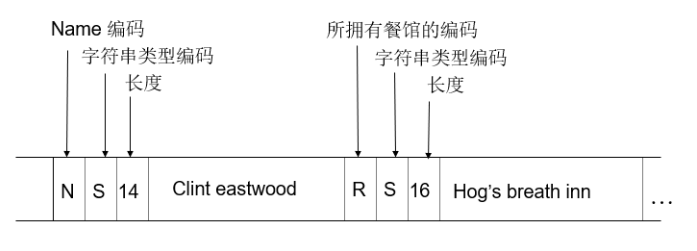
示例:假设要记录一个人的信息,包括姓名、投资的餐馆等,可能字段固定但是内容不固定。这个时候可以使用标记(如姓名)以及类型(如 string)加上长度来记录,例如下图中的 N 表示 name,S 表示 string 类型,14 表示 name 的长度。这样做的好处是即便不知道存储的格式,但是可以把一些特征标识保存起来,最后根据标识解析出数据。
1.3.3大值记录
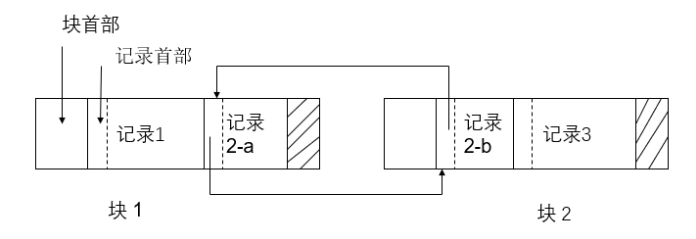
所谓大值,是指在一个块中无法存储的记录,大值涉及多个块之间的交互。
示例:如下图记录 2 存储时,分成了两部分进行存储,分别是记录 2-a 和记录 2-b,其中在存储记录 2-a 的时候,需要额外的存储空间来保存一些数据:一是标识,表明这是一个记录的片段;二是片段的序号,如这是第 1 个片段,或者第 N 个片段;最后还要保存指向下一个片段的指针,用于跨块之间的访问。
1.4缓冲池管理
对于数据库来说,其最大的开销一般是磁盘和内存之间IO交互,也就是将页面传输到内存所耗的那部分,减少磁盘访问次数的一种方法是在内存中保留尽可能多的页面,理想情况下,要访问的页面正好都已经在内存中了,这样就不再需要访问磁盘了。
1.3.1缓冲池结构
缓冲池是DBMS内部分配的一块内存区域,用来缓存从磁盘获取的页面。这片内存空间被组织为一个数组,其中每个数组项被称为一个帧(frame),一个帧正好能放置一个页面。类似于操作系统,当请求一个页面的时候首先先到缓冲池里面搜索,如果没有搜索到再从磁盘中获取并存入到缓冲池中的一个帧中。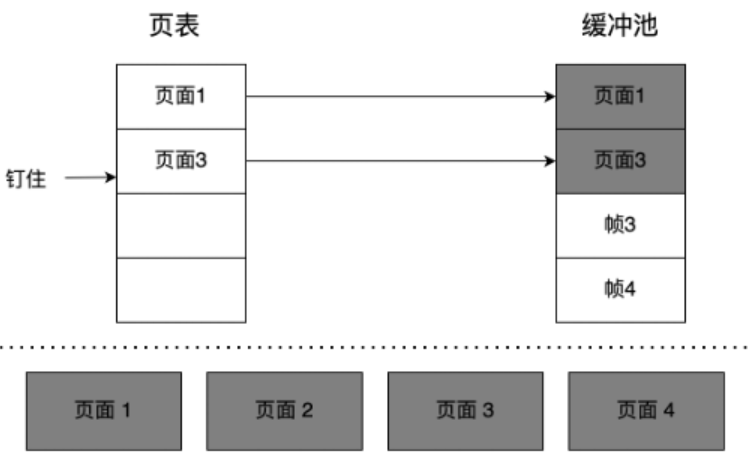
同样的,存在一个管理器来维护使用缓冲池所需要的元数据。存在页表,为一个内存哈希表(OS虚拟内存管理页表结构)对于64位系统,当我们得到一64位虚拟地址ip时,将前几位作为虚拟页码(前几位可能与页大小有关),计算虚拟页码的哈希值,计算出哈希值后到哈希表对应条目进行查找,哈希表使用链表来解决碰撞问题,每个链表节点有3个内容,虚拟页码,映射的帧码,下一个节点指针。在查找到帧码后将其与页偏移组合,得到真实物理地址用于登记当前已经在内存中的页面的信息。
页表将页面ID映射到缓冲池中一个帧的位置。因为缓冲池中页面的顺序不一定反映磁盘上的顺序,所以需要通过这个额外的数据结构来定位页面在缓冲池中的位置。除了最重要的内存地址之外,还需要为每个页面维护一个标志位和引用计数器(用于释放回收)。
脏标志:脏标志由线程在修改页面时设置。如果一个页面被设置了脏标志,就意味着缓冲池管理器必须将该页写回磁盘,以保证磁盘上的页面副本包含最新的数据。(修改位)
引用计数:引用计数表示当前访问该页(读取或修改该页)的线程数。线程在访问该页之前必须增加引用计数。如果页的引用计数大于零,说明该页面正在被使用,此时不允许缓冲池管理器从内存中淘汰该页。
关于缓冲池中的内存空间如何进行分配,一般采取两种策略:
全局策略:有利于当前整体工作负载的策略。全局策略综合考虑所有活动事务,以找到分配内存的最佳方案。
本地策略:以保证单个查询或事务运行得更快为目标的策略。本地策略将一个帧分配给特定事务时,不考虑其他并发事务的行为,即使这样可能对整体工作负载不利。
1.3.2缓冲池替换算法
DBMS对数据库文件的读写操作需要通过调用操作系统接口来实现,通常,为了优化I/O性能,操作系统自身也维护了一个缓冲区来缓存从磁盘读入的数据块。这个缓冲区和DBMS的缓冲池在功能上显然是重复的,会导致同一个数据库页面的数据在内存中的冗余存储,而且操作系统缓冲区的管理策略还使得DBMS难以控制内存与磁盘之间的页面交互。因此,大多数DBMS都使用直接I/O绕过操作系统的缓存。
因为需要DBMS来控制缓冲池,因此当需要释放一个帧为新页面腾出空间时,必须决定从缓冲池中淘汰掉哪个页面,替换算法的目标是提高正确性、准确性、速度和元数据开销。需要注意的是,引用计数大于零的页面是不能淘汰的。目前最常用的替换算法有最近最少使用(LRU)算法和时钟(CLOCK)算法。
LRU算法:LRU算法为每个页面维护其最后一次被访问的时间戳,这些时间戳可以存储在一个单独的数据结构(如队列)中,以便对其进行排序来提高效率。需要淘汰页面时,DBMS总是选择淘汰时间戳最早的页面。
CLOCK算法:CLOCK算法是一种近似LRU算法,它不需要每个页面都有单独的时间戳,而是为每个页面维护一个引用位。当某个页面被访问时,就将它的引用位的值置为1。想象页面被组织在循环缓冲区中,需要选择淘汰页面时,有一个”时钟指针”在循环缓冲区中扫描,检查页面的引用位是否为1。如果是,则将引用位重新置0并移动指针到下一个页面;否则,淘汰当前页面。
有三种解决方案可以解决LRU和CLOCK算法的缺点:
- 第一种解决方案是LRU-K,LRU-K中的K代表最近使用的次数,因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题,其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。它会以时间戳的形式登记最后K次引用的历史,并计算连续引用之间的时间间隔,将此历史记录用于预测页面下一次被访问的时间。
- 相比LRU,LRU-K需要多维护一个队列,用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候,才将数据放入缓存。当需要淘汰数据时,LRU-K会淘汰第K次访问时间距当前时间最大的数据。详细实现如下:
- 数据第一次被访问,加入到访问历史列表;
- 如果数据在访问历史列表里后没有达到K次访问,则按照一定规则(FIFO,LRU)淘汰;
- 当访问历史队列中的数据访问次数达到K次后,将数据索引从历史队列删除,将数据移到缓存队列中,并缓存此数据,缓存队列重新按照时间排序;
- 缓存数据队列中被再次访问后,重新排序;
- 需要淘汰数据时,淘汰缓存队列中排在末尾的数据,即:淘汰“倒数第K次访问离现在最久”的数据。
第二种解决方案是对每个查询进行局部化,DBMS在每个查询的局部范围内选择要淘汰的页面,这样可以最小化每个查询对缓冲池的污染。
最后一种解决方案是优先级提示,它允许事务在查询执行期间根据每个页面的上下文,告诉缓冲池管理器该页面是否重要。在淘汰页面时,对于脏页可以有两种处理方法:
- (1)总是优先淘汰缓冲池中的非脏页面;
- (2)先将脏页写回磁盘以确保其更改被持久化,然后再将其淘汰。后者会降低替换页面的速度;而前者虽然速度快,但是有可能将未来不会被再次访问的脏页留在缓冲池。
避免在淘汰页面时执行页面写出操作的一种方法是后台写。采用这种方法的DBMS会定期遍历页表并将脏页写入磁盘。当脏页被安全写入磁盘后,将该页面的脏标志重新置零。
1.3.3缓冲池的优化
- (1)多缓冲池
DBMS可以维护多个用于不同目的的缓冲池,比如每个数据库使用一个缓冲池,每种页面类型使用一个缓冲池。然后针对其中存储的数据的特点,每个缓冲池可以采用量身定制的管理策略。
将所需页面映射到缓冲池有两种方法:对象ID和散列。对象ID这种方法需要扩展元数据,使其包含关于每个缓冲池正在管理哪些数据库对象的信息,然后通过对象ID,就可以实现从对象到特定缓冲池的映射。另一种方法是散列,DBMS散列页面ID以选择访问哪个缓冲池。
(2)预取
DBMS还可以根据查询计划通过预取页面来进行优化。然后,在处理第一组页面时,系统可以将第二组页面预取到缓冲池中。这种方法通常在顺序访问多个页面时使用。(3)扫描共享
查询游标可以重用从磁盘读入的数据或操作符的计算结果,最大程度地减少多次扫描相同数据的开销。这种方法允许将多个查询附加到扫描表的单个游标上。当一个查询开始扫描时,如果已经有另一个查询在扫描,DBMS会将第一个查询附加到第二个查询的游标上。DBMS登记第二个查询加入时的位置,以便在到达数据结构末尾时结束扫描。换而言之,当多个查询需要执行相同的顺序扫描操作时,它们应该尽量共享已经加载到缓冲池中的数据页面,而不是每个查询都重新加载相同的数据。这可以通过缓存共享数据页面的内存块来实现,以便多个查询都可以访问相同的数据,从而减少磁盘 I/O 操作,提高性能。(4)缓冲池旁路
为了避免开销,顺序扫描操作符不会将获取的页存储在缓冲池中,而是使用正在运行的查询的本地内存。如果操作符需要读取磁盘上连续的大量页序列,那么这种方法可以很好地工作。缓冲池旁路也可以用于临时数据,如排序、连接。
1.3.4其他内存池
除了元组和索引,DBMS还需要内存来存放其他东西。这些内存池中的内容可能并不总是来自磁盘或者需要写入磁盘,具体取决于实现。
- 排序+连接缓冲区
- 查询缓存
- 维护缓冲区
- 日志缓冲区
- 字典缓存
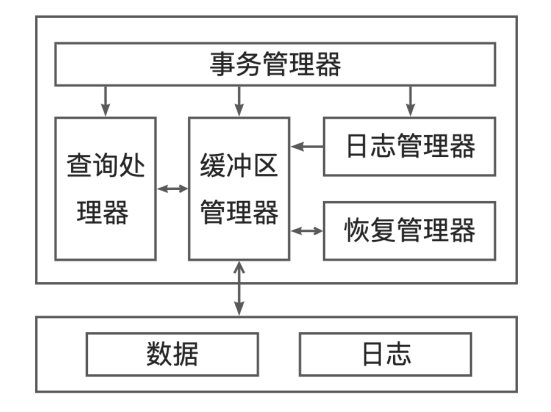
1.4数据库系统架构
事务管理器里面可以分为两个部分。
- 日志与恢复,所有的 SQL 在对磁盘进行操作的时候都会写一些日志,比如物理日志,逻辑日志,并且会提供一定的恢复功能,该部分负责事务的持久性。
- 并发控制,即怎么来控制对数据的事务,并发控制包括锁和 MVCC。并发控制负责保证事务的原子性和孤立性。
在存储层存在 Buffer Pool(缓冲池),所以不会直接从底层的磁盘中将数据提取出来。很多时候是通过 Buffer Pool 查询 Catalog,然后从 Catalog 中拿到所有的元数据信息,之后再发请求给存储管理器,由存储管理器最后发送到存储,然后从存储中将数据拿取出来。
1.5LRU-K补充
可以先去LeetCode把LRU这个数据结构给做了,网上也有不少对应的学习资料。
第二章 索引结构
2.1索引结构概述
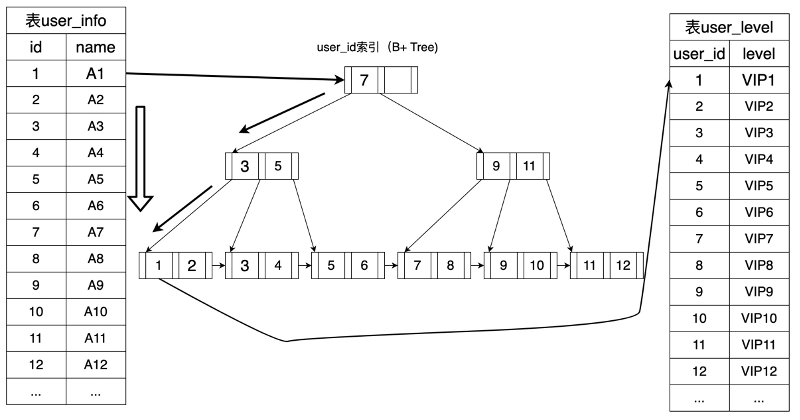
对于很多查询来说,只涉及表中的部分记录,例如寻找id为4的人,如果为了找这个人将整个表读取进将会损失很多效率,理想情况下DBMS能够直接定位到该记录。为了支持这种访问方式,需要额外设计一些与表相关联的附加结构,我们称之为索引。DBMS中最常用的索引结构为B+树与散列表。
索引是这样的数据结构:它以一个或多个属性的值为输入,并能快速地定位具有该值的记录的位置。建立索引的属性(组)称为查找键(search key)。与表一样,索引结构同样存储在数据库文件中。例如,我们可以用一个数据文件来存储一个表,用一个索引文件来存储一个索引。一个数据文件可能拥有一个或多个索引文件。除此之外,由于索引是指定表的附加结构,需要与表的内容保持一致,因此当表更新时,DBMS也需要同步更新表的索引。
在数据库中存在不同类型的索引结构,这些索引结构各自有自己的优势,评价索引结构一般参考以下指标:
- 查找类型:该索引结构能有效支持的查找类型,比如等值查找、范围查找等。
- 查找时间:使用该索引结构找到一个特定索引项(集)所需的时间。
- 插入时间:插入一个新的索引项所需的时间,包括找到插入这个新索引项的正确位置,以及更新索引结构所需的时间。
- 删除时间:删除一个索引项所需的时间,包括找到待删除项所需的时间, 以及更新索引结构所需的时间。
- 空间开销:索引结构所占用的存储空间。
2.2B+树
2.2.1B+树的结构
B+树是一种平衡排序树,树中根结点到叶结点的每条路径的长度相同,并且保持键的有序排列。在B+树中进行搜索、顺序访问、插入和删除的时间复杂度均为O(log(n)),它是在数据插入和删除的情况下仍能保持其执行效率的几种使用最广泛的索引结构之一,几乎所有现代DBMS都使用B+树。
B+树可以定义为具有以下性质的m路搜索树:
- 除非整棵树只有一个结点,否则根结点至少有两个子结点;
- 除根结点外的所有内结点至少是半满的,即有⌈m/2⌉到m个子结点;
- 所有叶结点的深度相等;
- 叶结点中键的数量必须大于等于 ⌈(m-1)/2⌉ 且小于等于 m-1 ;
- 每个有k个键的内结点都有k+1个非空子结点;
- 叶结点中包含所有查找键值。
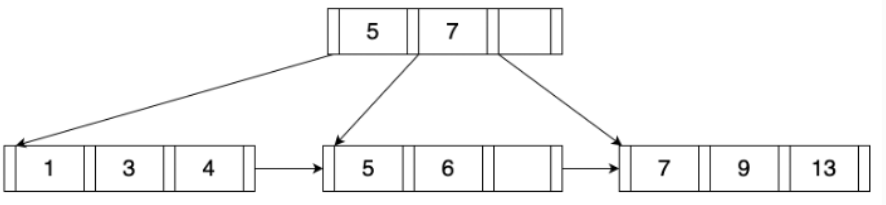
树中的每个结点都包含了一个键值对,并且是按键值排序的,一般来说键(key)来自索引的查找键,值则根据结点类型有不同含义。
如果结点是内结点,那么值则是指向子结点的指针。如果结点是叶结点,则结点汇总的值则可能是记录ID,比如对于DB种的非聚集索引,B+树中存放的就是记录位置的指针;叶结点中的值也可能是记录数据,比如对于聚集索引, B+树中存放的就是记录的实际数据。在树的最底层,叶结点间通过兄弟指针链接起来,形成一个按所有键值大小排序的链表,以便更高效地支持范围查找等顺序处理。
在上图中的B+树,m取值为4。具体实现上,把B+树索引存储到磁盘文件中的时候,通常是一个页面来存储一个结点,在页面空间能够允许的前提下应该把m取得尽可能的大,让树的高度降低来提高查询的效率。
2.2.2B+树的查找
2.2.2.1等值查找
对于一棵B+树,如果想找出键值为K的记录,则需要执行从根结点到叶结点的递归查找,查找过程为:
- 若当前结点为内结点,且结点中的键为K1,K2,…,Kn,则根据以下规则来决定下一步对此结点的哪一个子结点进行查找:
- 如果K<K1,则下一个结点为第1个子结点;
- 如果Ki≤K<Ki+1,则下一个结点为第i+1个子结点;
- 如果K≥Kn,则下一个结点为第n+1个子结点。
递归执行此查找过程,直到查找到叶结点,若当前结点为叶结点,在该结点的键值中查找,若第i个键值为K,则根据第i个值即可找到所需记录;否则查找失败。
2.2.2.2范围查找
如果想在B+树中找出在范围[a, b]之间的所有键值,先通过等值查找来查找键a,不论键a在B+树中是否存在,都会到达可能出现a的叶结点,然后在该叶结点中查找等于或大于a的那些键。只要在当前叶结点中不存在比b大的键,就根据兄弟指针找到下一个叶结点,继续查找[a, b]之间的所有键值。
上面的查找算法在查找范围只有上界或者只有下界时也有效:
- 当查找范围为[a,+∞)时,先找到键a可能出现的叶结点,然后从该结点中第一个等于或大于a的键开始,一直到最后一个叶结点的最后一个键。
- 当查找范围为(‐∞, b]时,则从B+树的第一个叶结点开始向后查找,直到遇到第一个超过b的键时停止查找。
2.2.3B+树的插入
向B+树中插入一个新索引项,必须遍历该树并使用内部结点来确定将键插入到哪个叶结点。在插入过程中,当结点太满时需要对其进行拆分,过程如下:
- 找到正确的叶结点L;
- 将新索引项按顺序插入到L中:
- 如果L有足够的空间,则执行插入操作,算法结束;
- 否则,将L平均拆分为L和L2两个结点,并复制L2的第一个键,将其插入到L的父结点中。
- 如果父结点中有足够的空间,则执行插入操作,算法结束;否则拆分父结点,将该结点的中间键上移插入到其父结点,然后将剩余的索引项平均拆分为两个结点。递归执行此步骤直到算法结束。
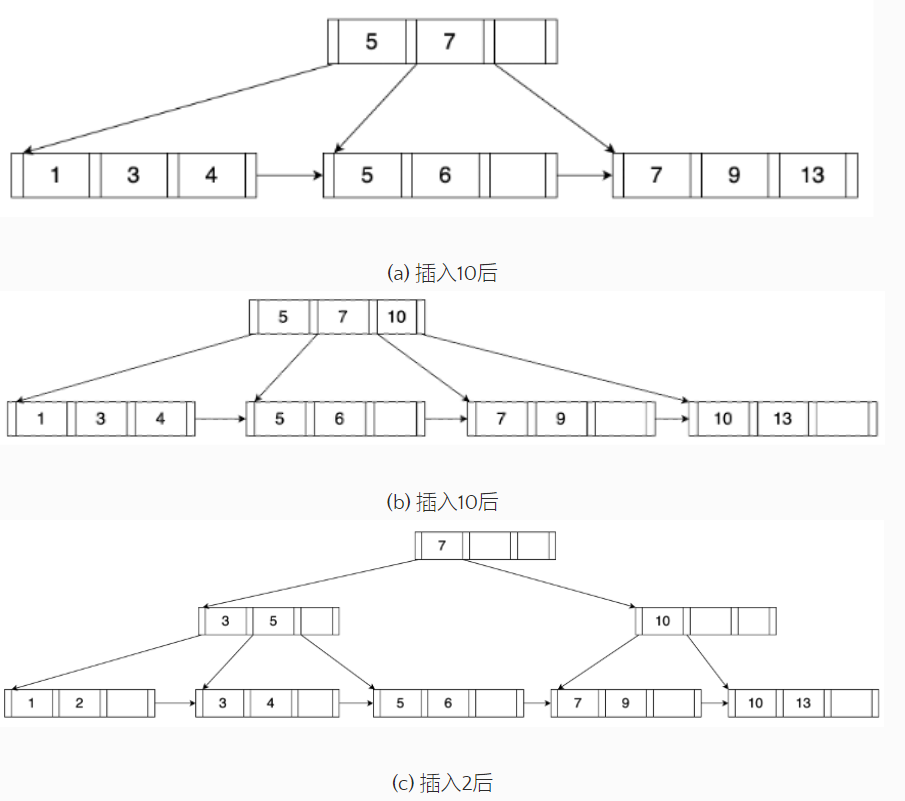
上图是向一棵4路B+树分别插入键值10和2的过程。可以看到,插入键值10后,原B+树中最右的叶结点发生了分裂,新增叶结点的第一个键值10被复制并插入到父结点中。插入键值2后,最左的叶结点发生了分裂,新增叶结点的第一个键值3被复制并插入到父结点中,而且还进一步导致了父结点的分裂,其中间键值7被上移并插入到新增的根结点中。
2.2.4B+树的删除
在删除过程中,如果因删除索引项导致结点小于半满状态,则必须合并结点。过程如下:
- 找到待删除的索引项所在的叶结点L;
- 从L中删除该索引项,删除后:
- 如果L不低于半满状态,则算法结束;
- 否则,通过向兄弟结点借索引项来满足约束条件,如果能成功借到,则算法结束;
- 如果兄弟结点也没有多余的索引项可借,则合并L和兄弟结点,删除父结点中指向被合并子结点的索引项。递归执行以上删除操作,直至算法结束。
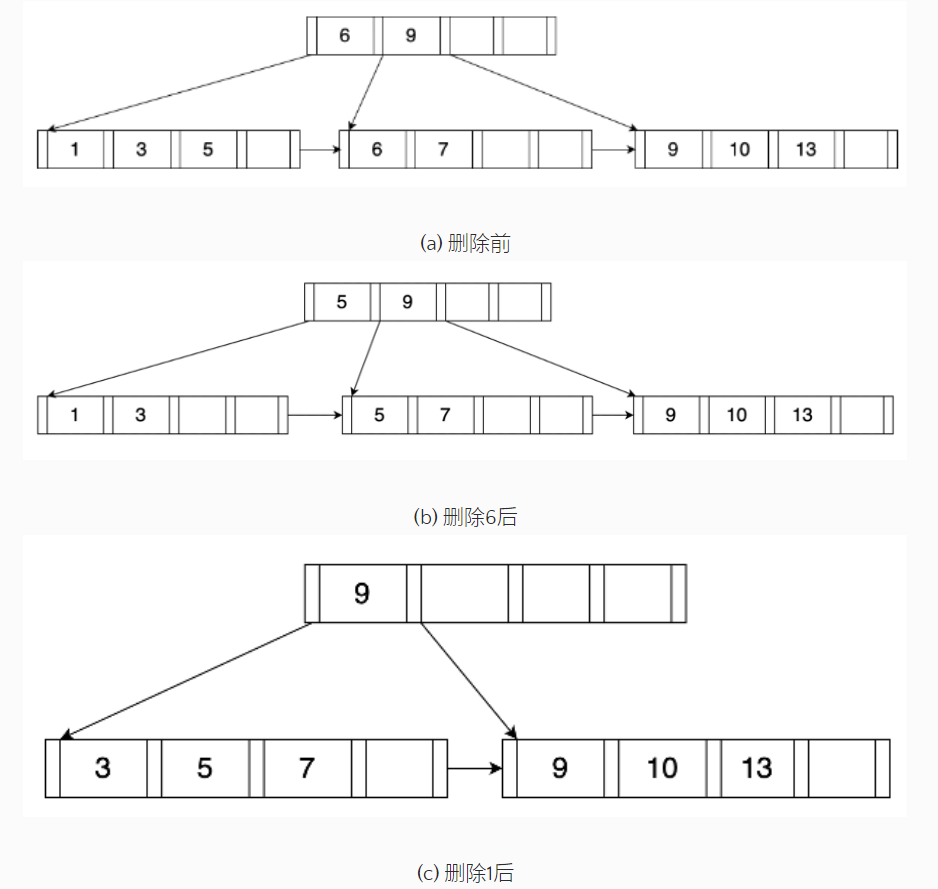
从一棵5路B+树中先后删除键值6和1的过程。可以看到,删除键值6时,原B+树中第二个叶结点中的项数已经无法满足最低要求,因此向左边的兄弟结点借了1项来达到约束条件。删除键值1时,最左的叶结点中项数无法满足最低要求,而且兄弟结点也没有多余的项可借,因此只能对最左的两个结点进行合并。
2.2.5非唯一查找键
基于某个查找键来构建索引时,假如表中存在两条或者多条记录在查找键属性上拥有相同的值,那么该查找键称为非唯一查找键。
非唯一查找键的一个问题在于影响记录删除的效率。假设某个查找键值出现了很多次,当表中拥有该查找键值的某条记录被删除时,为了维护索引与表数据的一致性,删除操作需要在B+树中查看很多个索引项,才能从中找出和被删除记录相对应的那个索引项并删除它,这个过程可能需要遍历多个叶结点。
解决以上问题的方法有两种:
一种简单的解决方法是创建包含原始查找键和其他额外属性的复合查找键,确保该复合查找键对于所有记录是唯一的,这种方法通常被大多数数据库系统使用。这个额外属性也叫唯一化属性,它可以是记录ID,或者是在拥有相同查找键值的所有记录中取值唯一的任何其他属性。删除一条记录时,先计算该记录的复合查找键值,然后再用这个复合键值到索引中查找。因为复合查找键值是唯一的,所以不会影响记录删除的效率。在这种方法中,一个查找键值在记录中出现多少次,它在索引中就会被重复存储多少次。
另一种方法是,每个查找键值在B+树中只存储一次,并且为该查找键值维护一个记录指针的桶(或者列表)来解决非唯一问题。这种方法虽然没有存储冗余信息,但是索引维护和修改起来更加复杂。
2.3散列表
散列表也叫哈希表,是一种常见的数据结构,它通过把键值映射到桶数组中的某个位置来加快查找记录的速度。散列表中包含两个关键元素:
- 散列函数 :散列函数h以查找键(散列键)为参数并计算出一个介于0到B-1之间的整数。
- 桶数组 :桶数组是一个编号从0到B-1、长度为B的数组,其中包含B个链表头,每个链表头对应一个桶,用于存储记录。
构造散列表时,如果一条记录的查找键为K,则将该记录链接到桶号为h(K)的桶中存储。
散列表在DBMS中被广泛运用,例如基于散列表来组织数据文件、基于散列表来构造索引文件、或者基于散列表进行连接运算等。当散列表的规模大到内存难以容纳时,或者出于数据持久化的目的,就需要将散列表存储在磁盘中。本教程主要讨论散列表在磁盘上的实现。
磁盘中的散列表与内存中的散列表存在一些区别。首先,桶数组是由页面组成,而不是由指向链表的指针组成;其次,散列到某个桶中的记录是存储在磁盘上的页面而非内存中。因此,磁盘上的散列表在设计时需要考虑访问磁盘的I/O代价以及表规模的扩展问题。
2.3.1静态散列表
对于一个散列表,如果其桶数组的规模B(即桶的数量)一旦确定下来就不再允许改变,则称其为静态散列表。
2.3.1.1散列函数
由于在设计时无法事先准确知道文件中将存储哪些搜索键值,因此我们希望选择一个具有下列特性的散列函数:
- 函数的输出是确定的。相同的搜索键值应该总是生成相同的散列值。
- 输出值的分布是随机且均匀的。散列函数应该表现为随机的,即散列值不应与搜索键的任何外部可见的排序相关,且不管搜索键值实际怎样分布,每个桶应分配到的记录数应该几乎相同。
- 易于计算。散列函数的执行时间不能太长,因为它需要执行很多次。
理想的散列函数是能将搜索键值均匀地分布到所有桶中,使每个桶含有相同数目的记录,但是这样的函数往往需要非常长的时间来进行计算。因此,散列函数需要在冲突率和快速执行之间进行权衡。目前最先进的散列函数是Facebook XXHash3。
2.3.1.2散列表的插入
当一个查找键为K的新记录需要被插入时,先计算h(K),找到桶号为h(K)的桶。如果桶内还有空间,我们就把该记录存放到此桶对应的页面中。如果该桶的页面中已经没有空间了,就增加一个新的溢出页,链接到该桶之后,并把新记录存入该页面。这种处理桶溢出问题的方式称为溢出链。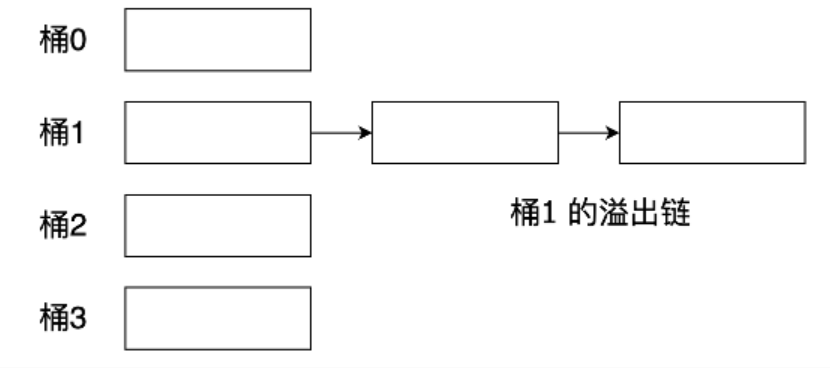
2.3.1.3散列表的删除
删除查找键值为K的记录与插入操作的方式类似。先找到桶号为h(K)的桶,由于不同的查找键值可能被映射到同一个桶中,因此还需要在桶内搜索,查找键值为K的记录,继而将找到的记录删除。删除记录后,如果允许记录在页面中移动,还可以选择合并同一桶链上的页面来减少链的长度。但是合并页面也有一定的风险,如果交替地往一个桶中插入和删除记录,可能导致页面被反复地创建和删除。
2.3.1.4散列表的效率
如果希望达到最好的查找效率,理想情况是散列表中有足够的桶,每个桶只由单个页面组成。如果是这样,那么查询一条记录就只需一次磁盘I/O,且记录的插入和删除也只需两次磁盘I/O。
为了减少桶溢出的可能性,桶的数量B可选为 (n/f)*(1+d),其中n是要存储的记录总数,f是一个桶中能存放的记录数,d表示避让因子,一般取值为0.2。这种做法会导致一定的浪费,平均每个桶有20%的空间是空的,好处则是减少了溢出的可能性。
但是,如果记录不断增长,而桶的数量固定不变,那么最终还是会出现很多桶都包含多个页面的情况。这种情况下,我们就需要在由多个页面构成的桶链中查找记录,每访问一个新的页面就增加一次磁盘I/O,这显然会严重影响散列表的查找效率。
2.3.2动态散列表
静态散列表由于其桶的数量不能改变,因此当无法预知记录总数时,难以解决由于记录数不断增长而带来的性能问题。本节我们将讨论两种动态散列表,它们能够以不同的方式动态调整散列表的大小,既不需要重新构建整个表,又能保证每个桶大多只有一个页面,从而最大化读写效率。
2.3.2.1可扩展散列表
与静态散列表相比,可扩展散列表在结构上做了以下改变:
- 增加了一个间接层,用一个指向页面的指针数组(桶地址表)而非页面数组来表示桶数组。
- 指针数组能动态增长,且数组长度总是2的幂,因此数组每增长一次,桶的数量就翻倍。
- 并非每个桶都单独拥有一个页面。如果多个桶的记录只需一个页面就能放下,那么这些桶可能共享一个页面,即多个桶指针指向同一个页面。
- 散列函数h为每个键计算出一个长度为N的二进制序列,N的值足够大(比如32),但是在某一时刻,这个序列中只有前i位(i≤N)被使用,此时桶的数量为 2i个。

向可扩展散列表中插入键值为K的记录的方法如下:
- 计算h(K),取出该二进制序列的前i位,并找到桶数组中编号与之相等的项,定位到该项对应的页面,假设该页面的编号为j;
- 如果页面j中还有剩余空间,则将该记录插入该页面,操作结束;
- 如果页面j已满,则需要分裂该页面:
a) 如果i=ij,说明在桶地址表中只有一个表项指向页面j,此时分裂该页,需要增加桶地址表的 大小,以容纳由于分裂而产生的两个桶指针。令i=i+1,使桶地址表的大小翻倍。桶地址表扩 展后,原表中的每个表项都被两个表项替代,且这两个表项都包含和原始表项一样的指针, 所以也应该有两个表项指向页面j。此时,分配一个新的页面n,并让第二个表项指向页面n。 将ij和in的值均置为当前的i值,并将原页面j中的各条记录重新散列,根据前i位来确定该记录 是放在页面j中还是页面n中,然后再次尝试插入新记录。极端情况下,新纪录要插入的页面 可能仍然是满的,说明原页面j中的所有记录在分裂后仍然被散列到了同一个页面中,此时需 要继续上述分裂过程,直至为新纪录找到可存放的空间。
b) 如果i> ij,说明在桶地址表中有多个表项指向页面j,此时不需要扩大桶地址表就能分裂页面 j。分配一个新的页面n,将ij和in置为原ij加1后的值;调整桶地址表中原来指向页面j的表项, 其中一半仍指向页面j,另一半则指向新创建的页面n;重新散列页面j中的各条记录,将其分 配到页面j或页面n中,并再次尝试插入新记录。与上一种情况一样,插入仍有可能失败,此 时需继续进行页面分裂的处理。
以下是一个可扩展散列表的例子。图1所示为一个小型的可扩展散列表,假设其散列函数h能产生4位二进制序列,即N=4。散列表只使用了1位,即i=1。此时桶数组只有2项,一个编号为0,一个编号为1,分别指向两个页面。第一页存放所有散列值以0开头的记录,第二页存放所有散列值以1开头的记录。每个页面上都标注了一个数字,表示由散列函数得到的二进制序列中的前几位用于判定记录在该页面中的成员资格。目前两个页面都只用了1位。
接下来向表中插人一个散列值为1010序列的记录。因为第一位是1,所以该记录应放入第二个页面,但第二页已经满了,因此需要分裂该页。而此时i2=i=l,因此先要将桶数组翻倍,令i=2,将数组的长度扩展为4。
扩展桶数组后,以0开头的两个项都指向存放散列值以0开头的记录的第一页,且该页上标注数字仍然为1, 说明该页中记录的成员资格只由其散列值的第一位判定。而原本存放散列值以1开头的记录的页面则需要分裂,把这个页面中以10开头和11开头的记录分别存放到两个页面中。在这两个页面上方标注的数字是2,表示该页面中记录的成员资格需要使用散列值的前两位来判定。改变后的散列表如图2所示。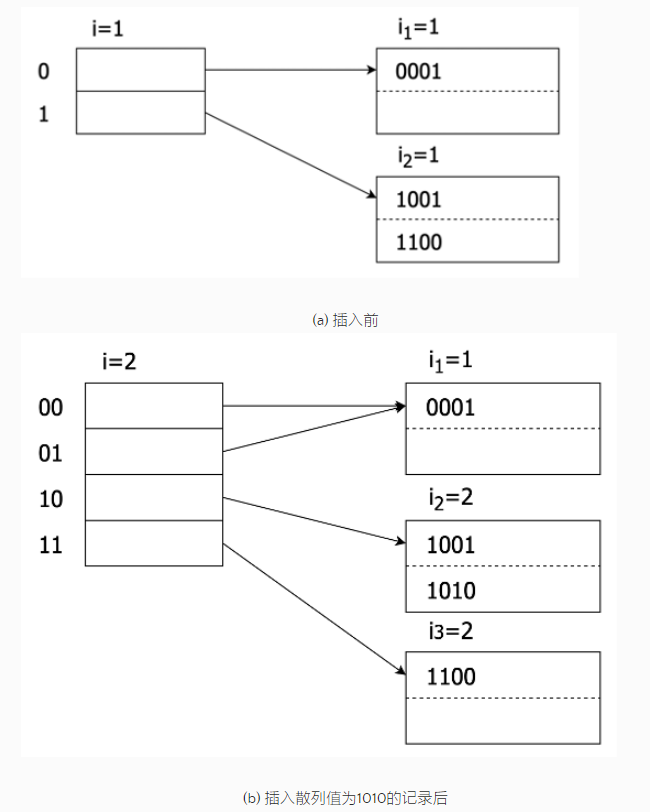
可扩展散列表的优点在于每个桶只有一个页面,所以如果桶地址表小到可以驻留在内存的话,查找一个记录最多只需要一次磁盘I/O。但是由于它是以桶数组翻倍的形式扩展的,所以也存在以下缺点:
- 随着i的增大,每次桶数组翻倍时需要做的工作将越来越多,而且这些工作还会阻塞对散列表的并发访问,影响插入和并发操作的效率。
- 随着i的增大,桶地址表会越来越大,可能无法全部驻留在内存,或者会挤占其他数据在内存中的空间,导致系统中的磁盘I/O操作增多。
2.3.2.2线性散列表
针对可扩展散列表存在的问题,下面介绍另一种动态散列表,称为线性散列表。相对于可扩展散列表,线性散列表中桶的增长较为缓慢,它有以下特点:
- 桶数n的大小,要能使所有桶中的实际记录总数与其能容纳的记录总数之间的比值保持在一个指定的阈值之下(如80%),如果超过该阈值,则增加一个新桶。
- 允许桶有溢出页,但是所有桶的平均溢出页数远小于1。
- 若当前的桶数为n,则桶数组项编号的二进制位数i=⌈ log2n⌉。
令一个线性散列表当前桶数为n,桶数组项编号的二进制位数为i,向线性散列表中插入键值为K的记录的方法如下:
- 计算h(K),取出该二进制序列右端的i位,假设为a1a2…ai,令a1a2…ai对应的二进制整数为m。如果m<n,说明编号为m的桶存在,将记录存入桶m中;如果n≤m<2i,说明编号为m的桶还不存在,则将记录存入编号为(m-2i-1)的桶中,即将a1a2…ai中的a1改为0时对应的桶。
- 如果要插入的桶中没有空间,则创建一个溢出页,将其链到该桶上,并将记录就存入该溢出块中。
- 插入记录后,计算 (当前实际记录总数r) / (n个桶能容纳的记录总数) 的值,并跟阈值相比,若超过阈值,则增加一个新桶到线性散列表中。注意,新增加的桶和之前发生插入的桶之间没有任何联系。如果新桶编号的二进制表示为la2a3…ai,则分裂桶号为0a2a3…ai的桶中的记录,根据这些记录的散列值的后i-1位分别散列到这两个桶中。
当n的值超过2i时,需要将i的值加1。理论上,对于现有的桶编号,要在它们的位序列前面增加一个0,来保证跟新的桶编号的位数一致,但是由于桶编号被解释成二进制整数,因此实际上它们只需要保持原样即可。
以下是一个线性散列表的例子。
图1所示为一个桶数n=2 的线性散列表,桶编号所需要的二进制位数i = ⌈ log22⌉ = 1,表中的记录数r=3。图中两个桶的编号分别为0和1,每个桶包含一个页面,每个页面能存放两个记录。假设散列函数产生4位二进制序列,用记录散列值的末位来确定该记录所属的桶,所有散列值以0结尾的记录放入第一个桶,以1结尾的记录放入第二个桶。
在确定桶数n时,本例使用的阈值是85%,即桶的平均充满率不超过总容量的85%。
下面先插入散列值为0101的记录。因为0101以1结尾,所以记录应放入第二个桶。插入该记录后,两个桶中存放了四个记录,平均充满率为100%,超过了85%,因此需要增加一个新桶,即桶数n=3。i = ⌈log23⌉ = 2,即桶编号需要2位。新增的桶的编号为10。接着,分裂桶00(即原来的桶0),将散列值为0000 (末两位为00)的记录保留在桶00中,散列值为1010(末两位为10)的记录存入桶10中,改变后的散列表如图2所示。
接下来再插入散列值为0001的记录。因为0001的末两位为01,所以应将该记录存入桶01中。不巧的是,该桶的页面已经装满,所以需要增加一个溢出页来提供存储空间。插入后,3个桶中有5条记录,平均充满率约83%,未超过85%,所以不需要创建新桶。改变后的散列表如图3所示。
2.4B+树补充
B树和B+树的目的是实现一个自组织的多级索引,B+树与B树相比,B+树的内部节点只存储键值对的键,而不存储数据。所有数据都存储在叶子节点中。叶子节点之间通过指针链接形成一个有序链表,以便支持范围查询。在插入和删除时,B树可能需要在内部节点中进行数据的移动,而B+树只需要在叶子节点中进行操作。
B+树的通过叶子结点的Pnext指针范围查询时,其IO读取次数不是一次。在B+树中,每一个叶子结点都是一页,即IO单位读取的字节大小,每遍历一个叶子节点时,都会有一次IO读取。
B+树相比B树减少了IO次数的真正原因:B+树的索引页不包含数据,因此一个数据页可查询到很多索引,降低下一次去磁盘再拿索引页的可能性。
对应的B+树也就是类似于操作系统中的多级索引,通过增加索引,用少量的存储空间来换取对应的快速查找,减少访问块拿取数据所耗的时间,使得一个块中尽可能多的包含所需的信息(无论是查找还是所需数据)。
为什么用B+树?InnoDB一棵B+树可以存放多少行数据?
这个问题的简单回答是:约2千万行。
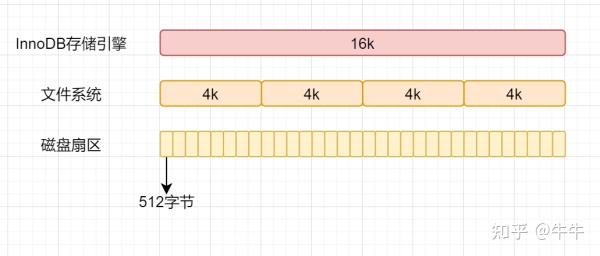
- 在计算机中,磁盘存储数据最小单元是扇区,一个扇区的大小是512字节。
- 文件系统中,最小单位是块,一个块大小就是4k;
- InnoDB存储引擎最小储存单元是页,一页大小就是16k。
因为B+树叶子存的是数据,内部节点存的是键值+指针。索引组织表通过非叶子节点的二分查找法以及指针确定数据在哪个页中,进而再去数据页中找到需要的数据;
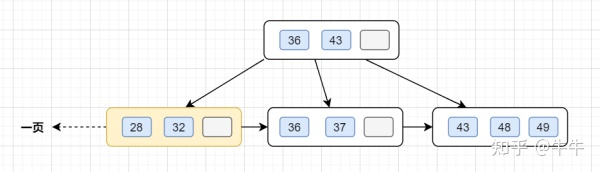
假设B+树的高度为2的话,即有一个根结点和若干个叶子结点。这棵B+树的存放总记录数为=根结点指针数*单个叶子节点记录行数。
- 如果一行记录的数据大小为1k,那么单个叶子节点可以存的记录数 =16k/1k =16.
- 非叶子节点内存放多少指针呢?我们假设主键ID为bigint类型,长度为8字节,而指针大小在InnoDB源码中设置为6字节,所以就是8+6=14字节,16k/14B =16*1024B/14B = 1170
因此,一棵高度为2的B+树,能存放1170 * 16=18720条这样的数据记录。同理一棵高度为3的B+树,能存放1170 *1170 *16 =21902400,也就是说,可以存放两千万左右的记录。B+树高度一般为1-3层,已经满足千万级别的数据存储。
2.4.1B+树的插入操作
在B+树中插入关键字时,需要注意以下几点:
- 插入的操作全部都在叶子结点上进行,且不能破坏关键字自小而大的顺序;
- 由于 B+树中各结点中存储的关键字的个数有明确的范围,做插入操作可能会出现结点中关键字个数超过阶数的情况,此时需要将该结点进行 “分裂”;
B+树的阶数 M = 3 ,且 ⌈M/2⌉ = 2(取上限) 、⌊M/2⌋ = 1(取下限),B+树的阶数是指一个B+树节点中最多可以包含的子节点数量(子树的数量),这个参数决定了B+树的节点大小以及树的结构,其中键的数量为阶数-1。
B+树中做插入关键字的操作,有以下 3 种情况:
- 1、 若被插入关键字所在的结点,其含有关键字数目小于阶数 M,则直接插入;
比如插入关键字 12 ,插入关键字所在的结点的 [10,15] 包含两个关键字,小于 M ,则直接插入关键字 12 。
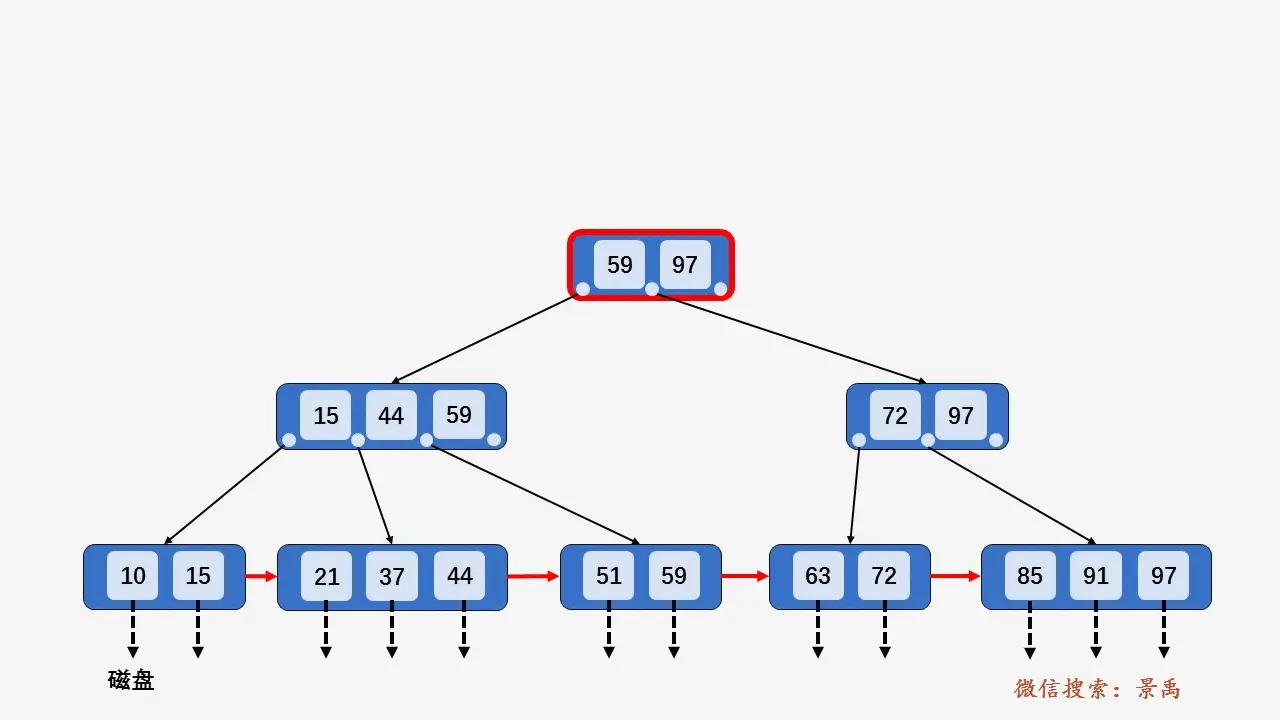
- 2、 若被插入关键字所在的结点,其含有关键字数目等于阶数 M,则需要将该结点分裂为两个结点,一个结点包含
⌊M/2⌋,另一个结点包含⌈M/2⌉。同时,将⌈M/2⌉的关键字上移至其双亲结点。假设其双亲结点中包含的关键字个数小于 M,则插入操作完成。
插入关键字 95 ,插入关键字所在结点 [85、91、97] 包含 3 个关键字,等于阶数 M ,则将 [85、91、97] 分裂为两个结点 [85、91] 和结点 [97] , 关键字 95 插入到结点 [95、97] 中,并将关键字 91 上移至其双亲结点中,发现其双亲结点 [72、97] 中包含的关键字的个数 2 小于阶数 M ,插入操作完成。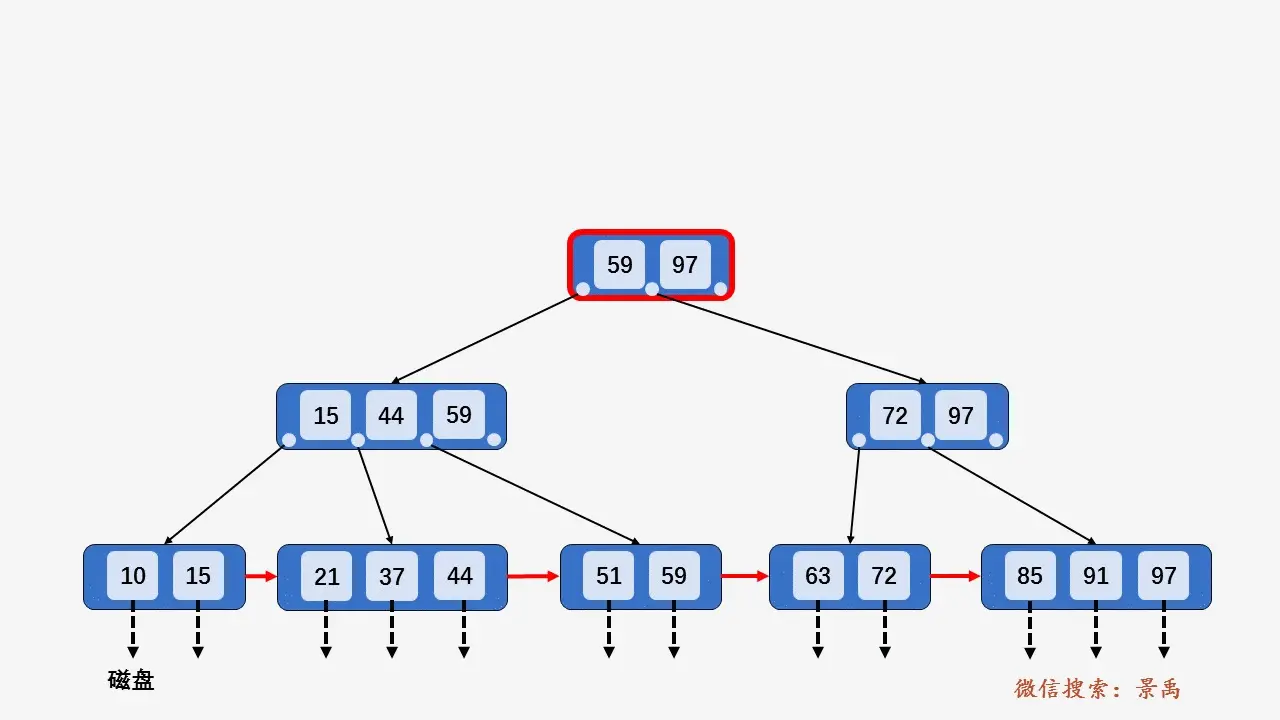
- 3、在第 2 情况中,如果上移操作导致其双亲结点中关键字个数大于 M,则应继续分裂其双亲结点。
插入关键字 40 ,按照第 2 种情况将结点分裂,并将关键字 37 上移到父结点,发现父结点 [15、37、44、59] 包含的关键字的个数大于 M ,所以将结点 [15、37、44、59] 分裂为两个结点 [15、37] 和结点 [44、59] ,并将关键字 37 上移到父结点中 [37、59、97] . 父结点包含关键字个数没有超过 M ,插入结束。

- 4、若插入的关键字比当前结点中的最大值还大,破坏了B+树中从根结点到当前结点的所有索引值,此时需要及时修正后,再做其他操作。
插入关键字 100,由于其值比最大值 97 还大,插入之后,从根结点到该结点经过的所有结点中的所有值都要由 97 改为 100。改完之后再做分裂操作。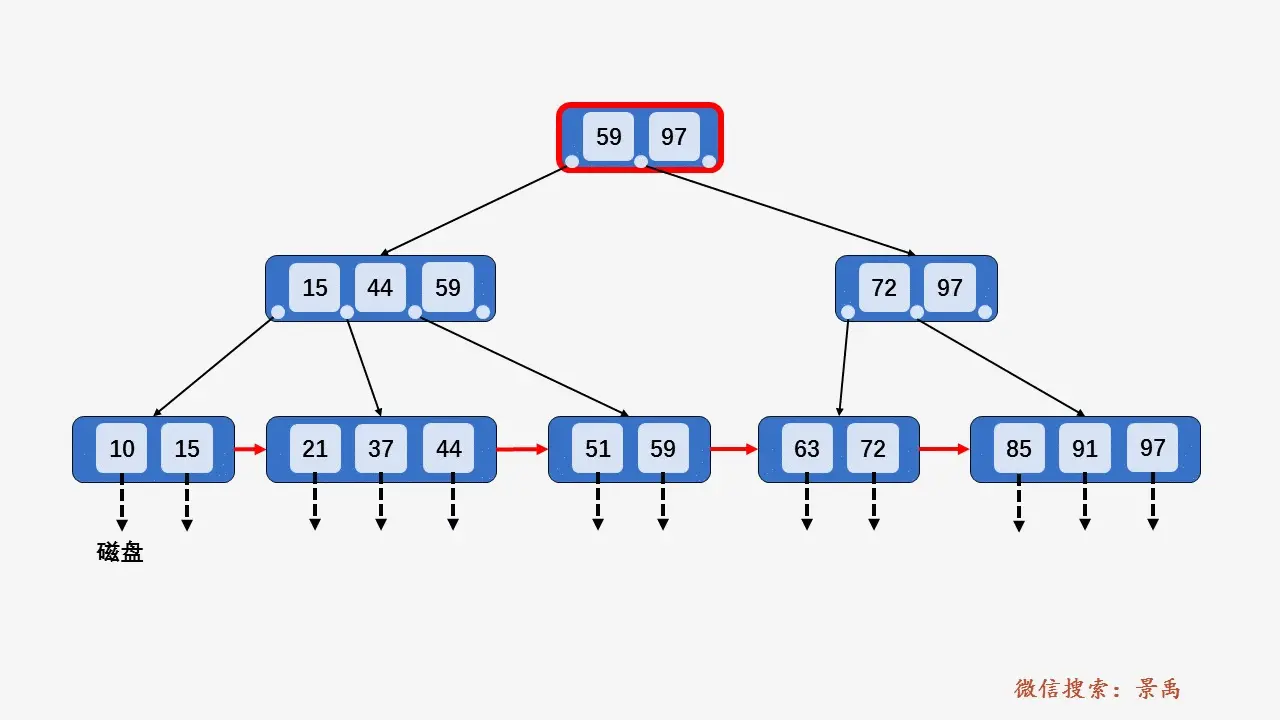
2.4.2B+树的删除操作
在 B+树中删除关键字时,有以下几种情况:
- 1、 找到存储有该关键字所在的结点时,由于该结点中关键字个数大于
⌈M/2⌉,做删除操作不会破坏 B+树,则可以直接删除。
删除关键字 91,包含关键字 91 的结点 [85、91、97] 中关键字的个数 3 大于 ⌈M/2⌉ = 2 ,做删除操作不会破坏 B+树的特性,直接删除。
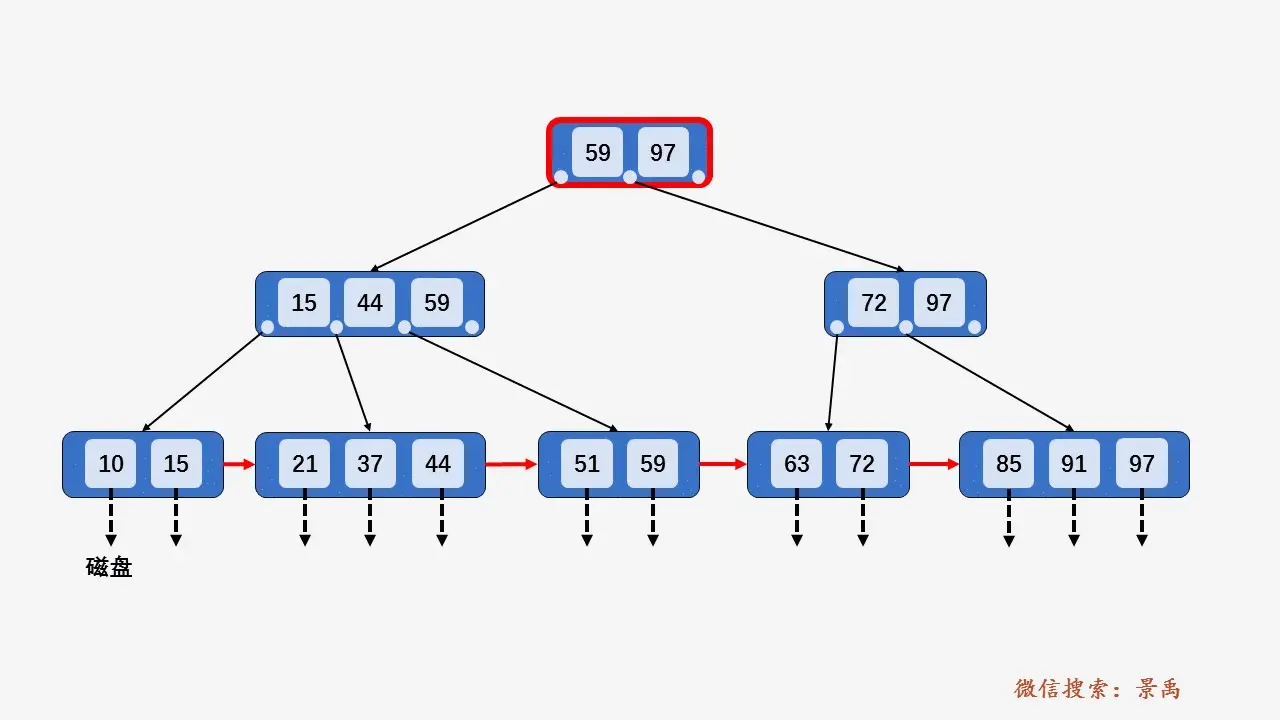
- 2、 当删除某结点中最大或者最小的关键字,就会涉及到更改其双亲结点一直到根结点中所有索引值的更改。
以删除整颗 B+树中最大的关键字 97 为例,查找并删除关键字 97 , 然后向上回溯,将所有关键字 97 替换为次最大的关键字 91 :

- 3、 当删除该关键字,导致当前结点中关键字个数小于
⌈M/2⌉,若其兄弟结点中含有多余的关键字,可以从兄弟结点中借关键字完成删除操作。
当删除某个关键字之后,结点中关键字个数小于 ⌈M/2⌉ ,则不符合 B+树的特性,则需要按照 3 he 4 两种情况分别处理。以删除关键字 51 为例,由于其兄弟结点 [21、37、44] 中含有 3 个关键字,所以可以选择借一个关键字 44,同时将双亲结点中的索引值 44 修改 37 ,删除过程如下图所示:

- 4、 第 3 种情况中,如果其兄弟结点没有多余的关键字,则需要同其兄弟结点进行合并。
为了说明这种情况,我们在第 3 种情况最终得到的 B+树之上进行删除操作。第 3 种情况删除关键字 51 之后得到如下所示 B+树: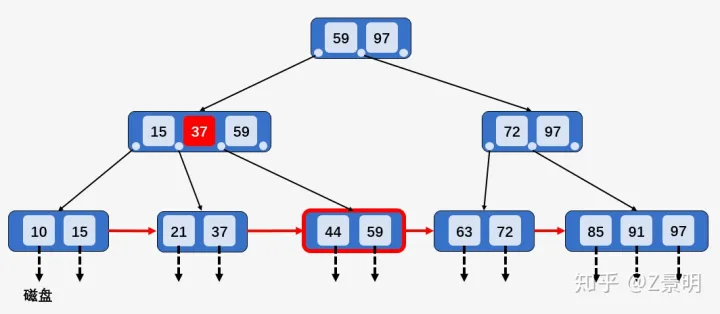
我们以删除上面这个 B+树中的关键字 59 说明第 4 种情况,首先查找到关键 59 所在结点 [44、59] ,发现该结点的兄弟结点 [21、37] 包含的关键字的个数 2 等于 ⌈M/2⌉, 所以删除关键字 59 ,并将结点 [21、37] 和 [44] 进行合并 [21、37、44] ,然后向上回溯,将所有关键字 59 替换为次最大的关键字 44 :
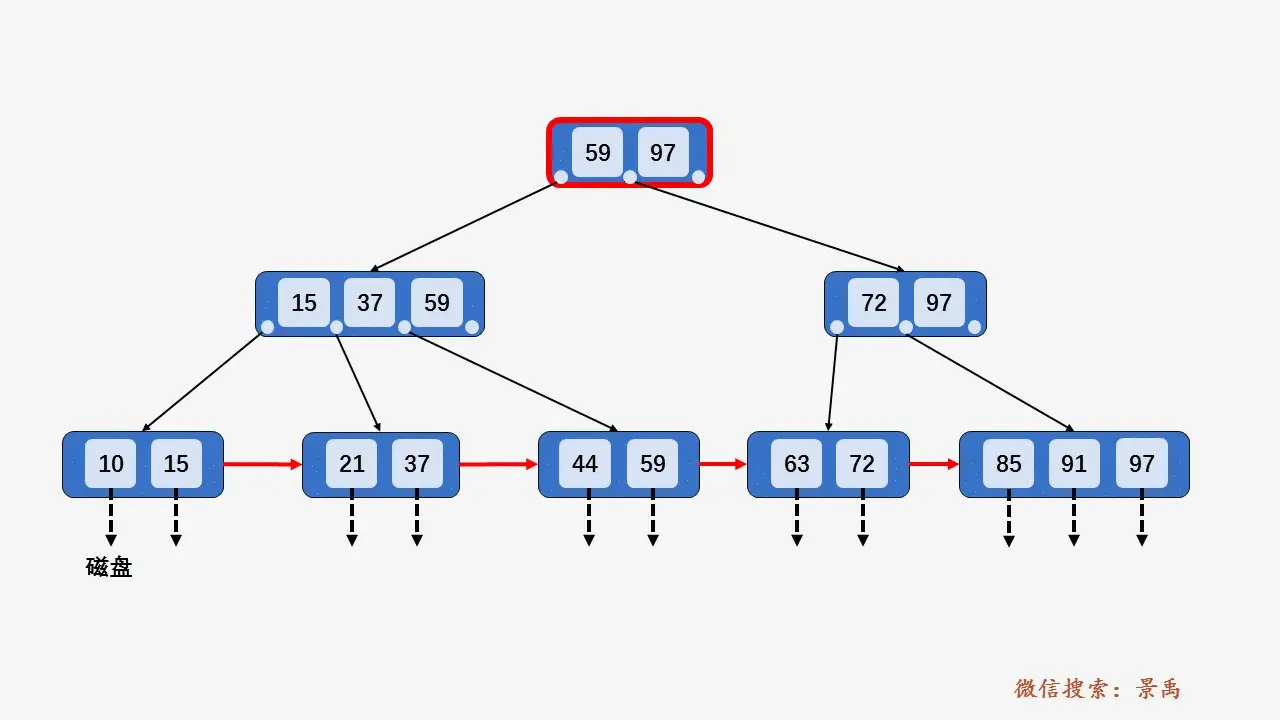
- 5、 当进行合并时,可能会产生因合并使其双亲结点破坏 B+树的结构,需要依照以上规律处理其双亲结点。
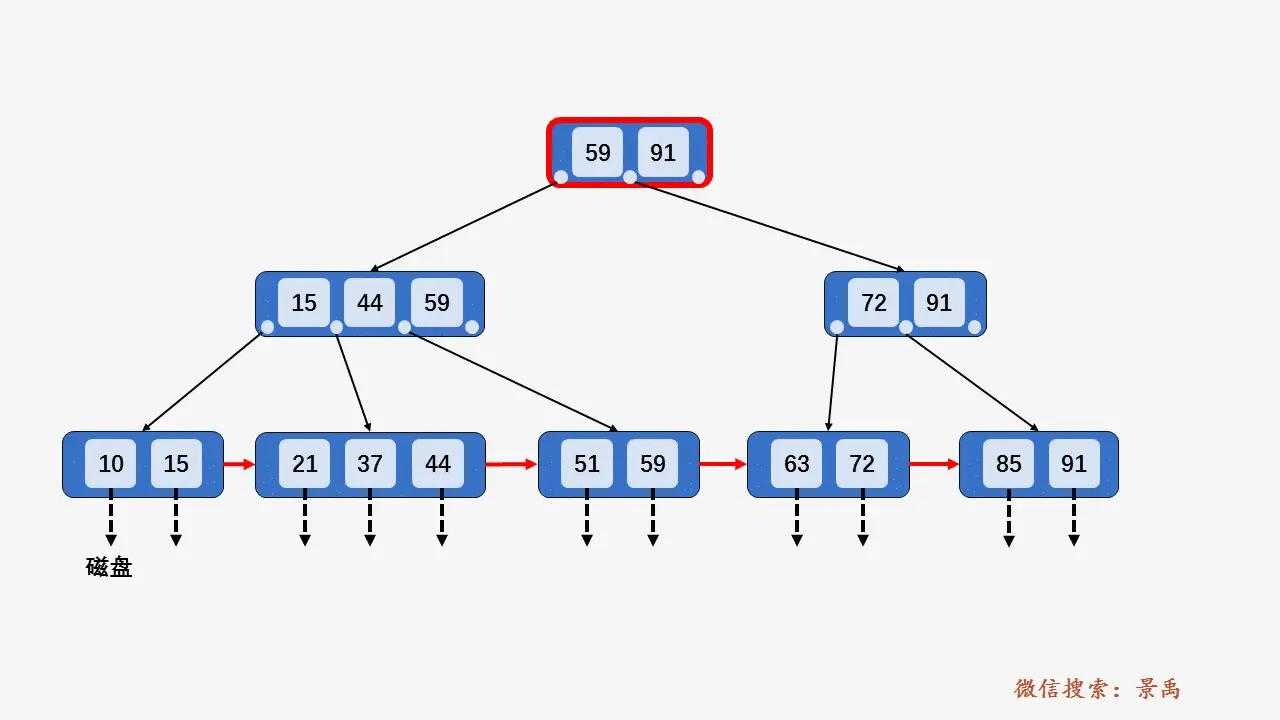
删除关键字 63,当删除关键字后,该结点中只剩关键字 72,且其兄弟结点 [85、91] 中只有 2 个关键字,所以将 [72] 和 [85、91] 进行合并,向上回溯,删除结点 [72、91] 当中的关键字 72 ,此时结点中只有关键 91 ,不满足 B+树中结点关键字个数要求,但其兄弟结点 [15、44、59] 中包含的 3 个关键字,所以从其兄弟结点当中借一个关键字 59 , 再对其兄弟结点的父结点中的关键字进行调整,将关键字 59 替换为 44 .
总之,在 B+树中做删除关键字的操作,采取如下的步骤:
- 删除该关键字,如果不破坏 B+树本身的性质,直接完成删除操作(情况 1);
- 如果删除操作导致其该结点中最大(或最小)值改变,则应相应改动其父结点中的索引值(情况 2);
- 在删除关键字后,如果导致其结点中关键字个数不足,有两种方法:一种是向兄弟结点去借,另外一种是同兄弟结点合并(情况 3、4 和 5)。(注意这两种方式有时需要更改其父结点中的索引值。)
2.5动态散列表补充
静态哈希有一个大前提就是我们事前是知道哈希表需要容纳多少键值对的,否则如果出现预设的容量过大或者过小问题时对其扩容或者缩容的代价都比较大(可以采用一致性哈希)。
因此,为了解决这个问题,提出了一些动态的哈希方案,即哈希表的运行的过程中可以按需增长或者减小。下面介绍三种动态哈希方案:
2.5.1 链式哈希
这是最简单的动态哈希方案,也是java或者jvm中默认的哈希方案。链式哈希中,哈希表中数组的成员是buckets的链表,因此,当发生冲突时,将元素添加到对应Bucket的末尾即可,如果Bucket已满,则创建一个新的Bucket即可。
2.5.2 可扩展哈希
链式哈希的一种改进,每个桶不再链式的生长,而是用分裂的方式来扩展,分裂的过程只会移动被分裂的桶中的元素,而不会影响其他的元素。
如下图所示,可扩展哈希方式包含一个slot数组和一系列的桶,每个slot中保存对应桶的指针。对于slot数组有一个全局bit位,记录在这个哈希表中需要多少位才能找到对应桶,对于每一个桶,有一个本地bit位,记录找到本地的桶需要多少位。
[注意]: 公式$$global_{bit} = \max(local_{bit})$$下图全局bit和本地bit的关系。
- Global Depth:假设global depth为n,那么当前的directory必定有 2� 个entry。例如,当前n=2,那么就有4个entry,n=3就有8个entry。同时,给定一个key,需要用global depth取出这个key的低n位的二进制值。例如,一个key的二进制是10111,如果global depth是3,通过
IndexOf(key)函数,得到返回值的二进制值是111,即为7。这个值用来索引directory[111]位置的bucket。 - Local Depth:local depth指的是(假设local depth为n),在当前的bucket之下,每个元素的key的低n位都是相同的。
两者之间有什么关系呢?
- 对于一个bucket来说,如果当前的global depth等于local depth,那说明这个bucket只有一个指针指向它。
- 如果当前的global depth大于local depth,必定不止一个指针指向它。
- 计算当前bucket有几个指针指向它的公示是$2^{globalDepth-localDepth}$ 。

关于对应的entry的增长,这一步有一个很重要的点,新增长的entry怎么分配到对应的bucket?如果和上图的情况一样,从1增长到2,只需要把多出来的一个拉到唯一的bucket上就可以了,但如果从2到4,从4到8呢?多出来的若干个如何处理?其实只需要将多出来的一部分指针完全复制之前的一份就可以了。
这样做法我觉得是可扩展哈希的比较重要的细节,由于可扩展哈希扩展direcotry时是按照当前大小的两倍进行扩展,新增长出来的部分作为之前directory的对等实体,每一个新的entry都对应了之前对应的entry,指向相同的bucket。唯一的不同就是之前的direcotry的索引最高位是0,扩展出来的最高位是1。

一个比较好的解释可以看这份实验解说,讨论了可拓展哈希表的一些细节。
2.5.3 线性哈希
线性哈希是可扩展哈希的改进,可扩展哈希有一个小的性能瓶颈,在桶分裂且需要扩展slot array时,需要对整个slot array加锁直到桶分裂完成。为了解决这个问题,提出了线性哈希方式。哈希表维护一个指针,指向下一个准备分裂的桶,并且线性哈希采用多个哈希函数来寻找正确的桶。
当插入过程中,任何一个桶溢出,都将分裂指针指向桶(无论这个桶是否溢出)。最初,指针指向第一个桶,即当任何一个桶发生溢出时,都分裂第一个桶。且现在只有一个哈希函数。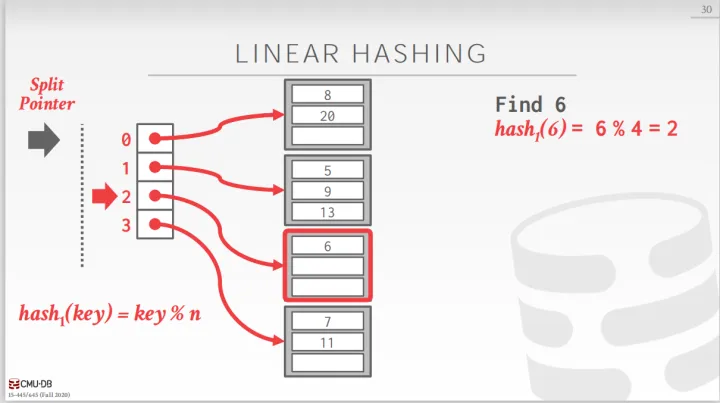
现需要插入17,发现对应的桶已满,发生了溢出,因此需要分裂第一个桶.

现在将第一个桶分裂,就需要增加一个桶,那么哈希表中已经有了5个桶,原来的哈希函数中的n为4,不能满足使用要求,需要增加新的哈希函数$ℎasℎ_2$。然后使用新的哈希函数重新分配第一个桶中的元素。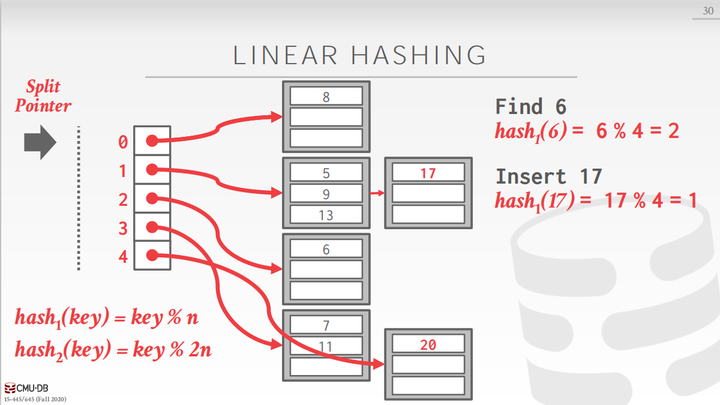
现在再来观察查询过程,现在需要查询20,首先使用第一个哈希函数,发现哈希值为0,即第一个桶。但是这个哈希值落在了分裂指针的上面,即要查询的值落在一个已经分裂的桶上,而这个桶中的所有键值对已经用第二个哈希函数重新分配位置,因此,需要用第二个哈希函数重新计算哈希值为4,即第五个桶中,然后在这个桶中循序查询即可。
2.6SQL索引背后
MySQL官方对索引的定义为:索引(Index)是帮助MySQL高效获取数据的数据结构。提取句子主干,就可以得到索引的本质:索引是数据结构。因为数据本身的组织结构不可能完全满足各种数据结构(例如,理论上不可能同时将两列都按顺序进行组织),所以,在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用(指向)数据,这样就可以在这些数据结构上实现高级查找算法。这种数据结构就是索引。

以上图为例子,左边是数据表,一共有两列七条记录,最左边的是数据记录的物理地址(注意逻辑上相邻的记录在磁盘上也并不是一定物理相邻的)。为了加快Col2的查找,可以维护一个右边所示的二叉查找树,每个节点分别包含索引键值和一个指向对应数据记录物理地址的指针,这样就可以运用二叉查找在(O(log_2n))的复杂度内获取到相应数据。
2.6.1为什么使用B+Tree
一般来说,索引本身也很大,不可能全部存储在内存中,因此索引往往以索引文件的形式存储的磁盘上。这样的话,索引查找过程中就要产生磁盘I/O消耗,相对于内存存取,I/O存取的消耗要高几个数量级,所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的渐进复杂度。换句话说,索引的结构组织要尽量减少查找过程中磁盘I/O的存取次数。下面先介绍内存和磁盘存取原理,然后再结合这些原理分析B-/+Tree作为索引的效率。
2.6.1.1主存存取原理
目前计算机使用的主存基本都是随机读写存储器(RAM),现代RAM的结构和存取原理比较复杂,这里本文抛却具体差别,抽象出一个十分简单的存取模型来说明RAM的工作原理。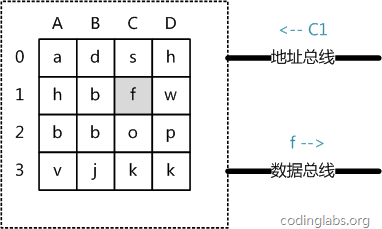
从抽象角度看,主存是一系列的存储单元组成的矩阵,每个存储单元存储固定大小的数据。每个存储单元有唯一的地址,这里将其简化成一个二维地址:通过一个行地址和一个列地址可以唯一定位到一个存储单元。
主存的存取过程如下:
- 当系统需要读取主存时,则将地址信号放到地址总线上传给主存,主存读到地址信号后,解析信号并定位到指定存储单元,然后将此存储单元数据放到数据总线上,供其它部件读取。
- 写主存的过程类似,系统将要写入单元地址和数据分别放在地址总线和数据总线上,主存读取两个总线的内容,做相应的写操作。
- 这里可以看出,主存存取的时间仅与存取次数呈线性关系,因为不存在机械操作,两次存取的数据的“距离”不会对时间有任何影响,例如,先取A0再取A1和先取A0再取D3的时间消耗是一样的。
2.6.1.2磁盘存取原理
索引一般以文件形式存储在磁盘上,索引检索需要磁盘I/O操作。与主存不同,磁盘I/O存在机械运动耗费,因此磁盘I/O的时间消耗是巨大的。
一个磁盘由大小相同且同轴的圆形盘片组成,磁盘可以转动(各个磁盘必须同步转动)。在磁盘的一侧有磁头支架,磁头支架固定了一组磁头,每个磁头负责存取一个磁盘的内容。磁头不能转动,但是可以沿磁盘半径方向运动(实际是斜切向运动),每个磁头同一时刻也必须是同轴的,即从正上方向下看,所有磁头任何时候都是重叠的(不过目前已经有多磁头独立技术,可不受此限制)。

盘片被划分成一系列同心环,圆心是盘片中心,每个同心环叫做一个磁道,所有半径相同的磁道组成一个柱面。磁道被沿半径线划分成一个个小的段,每个段叫做一个扇区,每个扇区是磁盘的最小存储单元。为了简单起见,我们下面假设磁盘只有一个盘片和一个磁头。
当需要从磁盘读取数据时,系统会将数据逻辑地址传给磁盘,磁盘的控制电路按照寻址逻辑将逻辑地址翻译成物理地址,即确定要读的数据在哪个磁道,哪个扇区。为了读取这个扇区的数据,需要将磁头放到这个扇区上方,为了实现这一点,磁头需要移动对准相应磁道,这个过程叫做寻道,所耗费时间叫做寻道时间,然后磁盘旋转将目标扇区旋转到磁头下,这个过程耗费的时间叫做旋转时间。在得到对应块后,再在对应的块内部通过偏移量得到所需的字节。
局部性原理与磁盘预读
由于存储介质的特性,磁盘本身存取就比主存慢很多,再加上机械运动耗费,磁盘的存取速度往往是主存的几百分分之一,因此为了提高效率,要尽量减少磁盘I/O。为了达到这个目的,磁盘往往不是严格按需读取,而是每次都会预读,即使只需要一个字节,磁盘也会从这个位置开始,顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理:
当一个数据被用到时,其附近的数据也通常会马上被使用。程序运行期间所需要的数据通常比较集中。由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高I/O效率。
预读的长度一般为页(page)的整倍数。页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,每个存储块称为一页(在许多操作系统中,页得大小通常为4k),主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
2.6.2MySQL索引实现
在MySQL中,索引属于存储引擎级别的概念,不同存储引擎对索引的实现方式是不同的,本文主要讨论MyISAM和InnoDB两个存储引擎的索引实现方式。
2.6.2.1 MyISAM索引实现
MyISAM引擎使用B+Tree作为索引结构,叶节点的data域存放的是数据记录的地址。下图是MyISAM索引的原理图: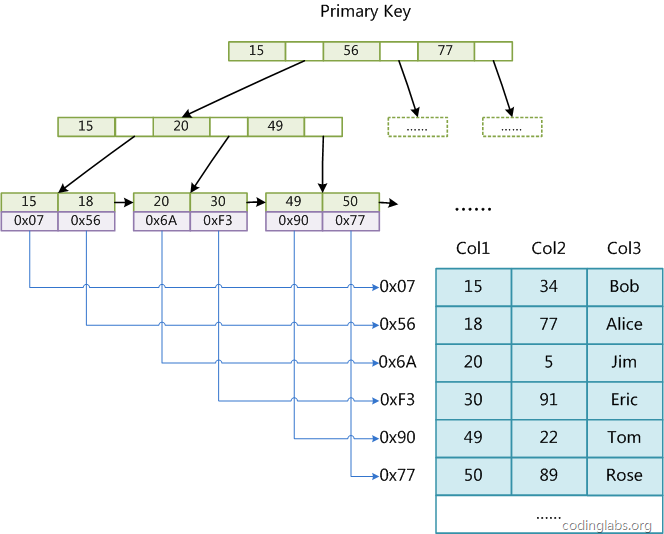
这里设表一共有三列,假设我们以Col1为主键,则图8是一个MyISAM表的主索引(Primary key)示意。可以看出MyISAM的索引文件仅仅保存数据记录的地址。在MyISAM中,主索引和辅助索引(Secondary key)在结构上没有任何区别,只是主索引要求key是唯一的,而辅助索引的key可以重复。如果我们在Col2上建立一个辅助索引,则此索引的结构如下图所示: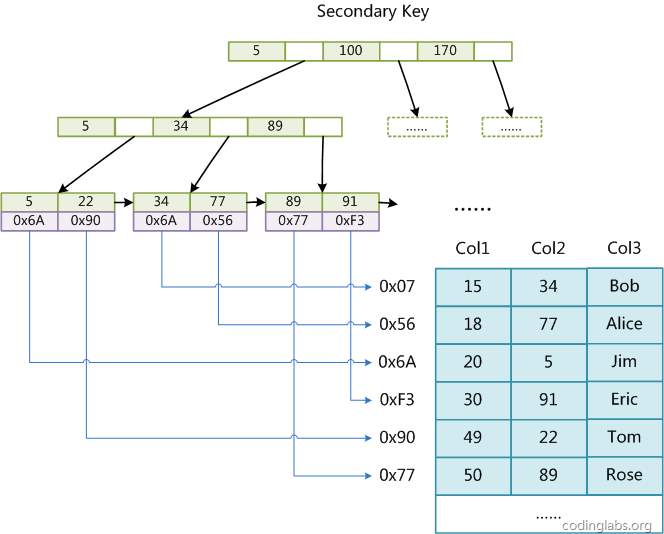
同样也是一颗B+Tree,data域保存数据记录的地址。因此,MyISAM中索引检索的算法为首先按照B+Tree搜索算法搜索索引,如果指定的Key存在,则取出其data域的值,然后以data域的值为地址,读取相应数据记录。MyISAM的索引方式也叫做“非聚集”的,之所以这么称呼是为了与InnoDB的聚集索引区分。
2.6.2.2InnoDB索引实现
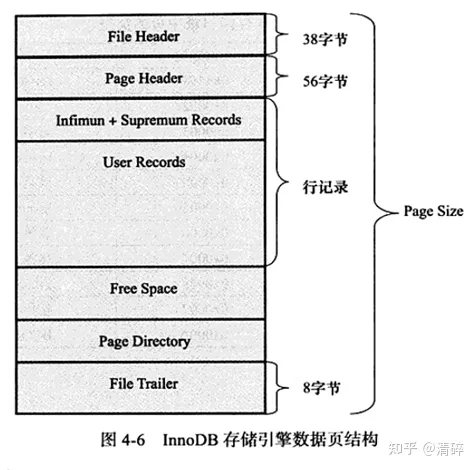
虽然InnoDB也使用B+Tree作为索引结构,但具体实现方式却与MyISAM截然不同。第一个重大区别是InnoDB的数据文件本身就是索引文件。从上文知道,MyISAM索引文件和数据文件是分离的,索引文件仅保存数据记录的地址。而在InnoDB中,表数据文件本身就是按B+Tree组织的一个索引结构,这棵树的叶节点data域保存了完整的数据记录。这个索引的key是数据表的主键,因此InnoDB表数据文件本身就是主索引。
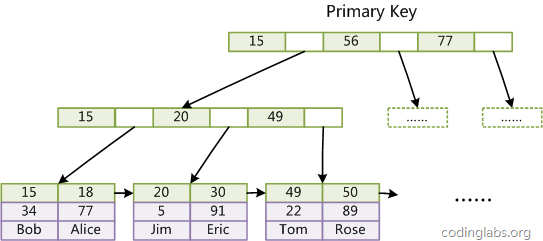
上图是InnoDB主索引(同时也是数据文件)的示意图,可以看到叶节点包含了完整的数据记录。这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集,所以InnoDB要求表必须有主键(MyISAM可以没有),如果没有显式指定,则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键,如果不存在这种列,则MySQL自动为InnoDB表生成一个隐含字段作为主键,这个字段长度为6个字节,类型为长整形。
第二个与MyISAM索引的不同是InnoDB的辅助索引data域存储相应记录主键的值而不是地址。换句话说,InnoDB的所有辅助索引都引用主键作为data域。例如,下图为定义在Col3上的一个辅助索引: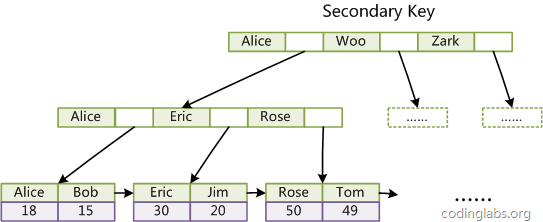
这里以英文字符的ASCII码作为比较准则。聚集索引这种实现方式使得按主键的搜索十分高效,但是辅助索引搜索需要检索两遍索引:首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录。
了解不同存储引擎的索引实现方式对于正确使用和优化索引都非常有帮助,例如知道了InnoDB的索引实现后,就很容易明白为什么不建议使用过长的字段作为主键,因为所有辅助索引都引用主索引,过长的主索引会令辅助索引变得过大。再例如,用非单调的字段作为主键在InnoDB中不是个好主意,因为InnoDB数据文件本身是一颗B+Tree,非单调的主键会造成在插入新记录时数据文件为了维持B+Tree的特性而频繁的分裂调整,十分低效,而使用自增字段作为主键则是一个很好的选择。
- 聚簇索引:数据是按照主键索引组织,也就是行的数据聚集在了主键索引里面。即主键B+树的叶子结点结构和磁盘上存储的文件页是相同的,方便扫描搜索。
- 非聚簇索引:主键索引本身是key和数据存储位置,即存储的是页号与slot号的索引。
对于高效的存储介质,可以把B+树节点大小设置小一点,因为这样可以尽量减少读取的冗余数据。
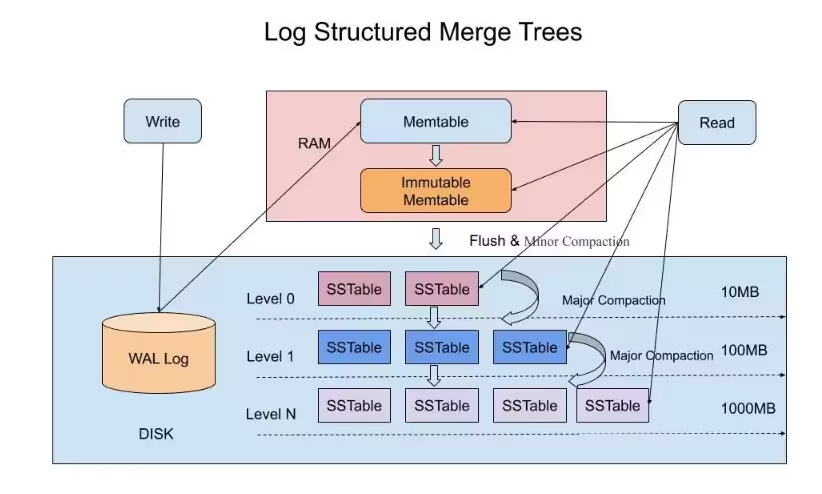
2.7LSM-Tree
LSM-Tree 的全称为日志结构合并树〈Log-Structured Merge Tree),核心思想是将内存中的缓存数据以记录日志的形式追加写入到存储介质,初衷是为了将小粒度的随机写聚合成大粒度的顺序追加写,从而减少机械磁盘悬臂的频繁机械运动,提升I/O效率。
具体来说 LSM 的数据更新是日志式的,修改数据时直接追加一条新记录(为被修改数据创建一个新版本),而使用 B/B+ 树的数据库则需要找到数据在磁盘上的位置并在原地进行修改。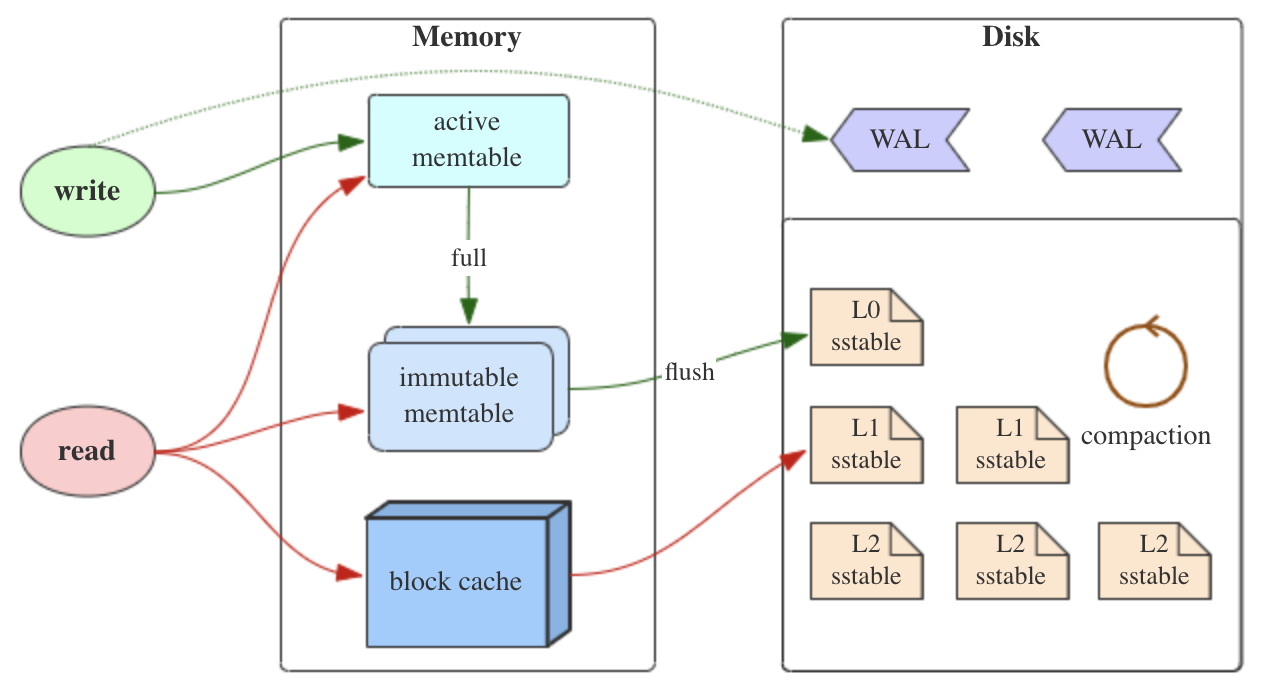
LSM-Tree 的基本结构如上图,数据被分成了多层,其中CO存储在内存,其他层存储在外存,数据在每一层按照Key的大小依次排列,并且这些层的容量依次成倍增加。
LSM 树将离散的随机写请求都转换成批量的顺序写请求(WAL + memtable),以此提高写性能。但也带来了一些问题:
- 读放大(Read Amplification)。按照上面【读操作】的描述,读操作有可能会访问大量的文件;
- 空间放大(Space Amplification)。因为所有的写入都是顺序写(Append-only)的,不是在对数据进行直接更新(in-place update),所以过期数据不会马上被清理掉
所以维护和减少 SST 文件数量是很有必要的。RocksDB 会根据配置的不同 Compaction 算法策略,进行 Compaction 操作。Compaction 操作会删除过期 或者标记为删除/重复的 key,对数据进行重新合并来提高查询效率。
当键值对写入LSM-Tree时,首先会被插入到位于内存中的C0,当C0满了以后,C0中的数据会和C1中的数据进行合并,合并后的结果会重新写入C1。同理,当Cn满了时,Cn也会和Cn+1合并,合并后的结果写入Cn+1。这些合并操作被称为Compaction操作。
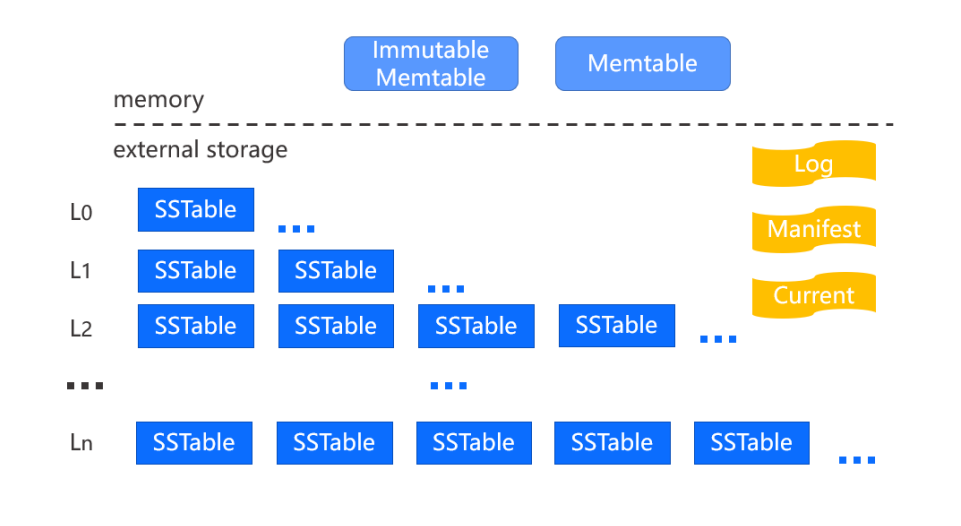
比如常见的LevelDB中就使用了这一数据结构,如前文中提到的,对于LSM-Tree而言维护着内存外存两部分,分别是在内存的Memtable(内存表)部分和Inmutable Memtable(只读内存表)两部分,即前文的c0。
另一部分存储在外存,同时按存储的量级上升,其中外存部分每层有Sorted string table(顺序字符串表)文件,其中k-v数据就存储在这些SSTable文件中,除了L0其他层都是按key的顺序排列的,也就是层间存放的key范围是不重叠的。
除了数据,LevelDB还有Log、Mainfest以及Current文件:
- Log 文件存储最近的数据更新,采用追加的方式将每次的更新数据写到日志文件的末尾,每个日志文件对应当前的Memtable,更新操作先写入日志文件然后更新内存表。当内存表被写入SSTable 文件后,相应的日志文件会被删除。Log 文件也可做故障恢复。
- Mainfest文件存储当前数据库元数据,如每层包含哪些SSTable文件、每个文件中 key的范围以及其他的元数据信息,如日志文件等。
- Current文件是一个简单的文本文件,记录当前使用的Mainfest文件名,通常通过判断当前文件是否存在来判断数据库是否已经创建。
Compaction 虽然减少了读放大(减少 SST 文件数量)和空间放大(清理无效数据),但也因此带来了写放大(Write Amplification)的问题(底层 I/O 被 Compaction 操作消耗,会大于上层请求速递)
LevelDB的数据写入流程可以理解为两步:
- 追加一条日志记录到Log 文件。
- 写入Memtable,其中 Memtable被实现为跳表,跳表的功能和平衡树类似,但实现更为简单,并且维持平衡的操作更轻量。
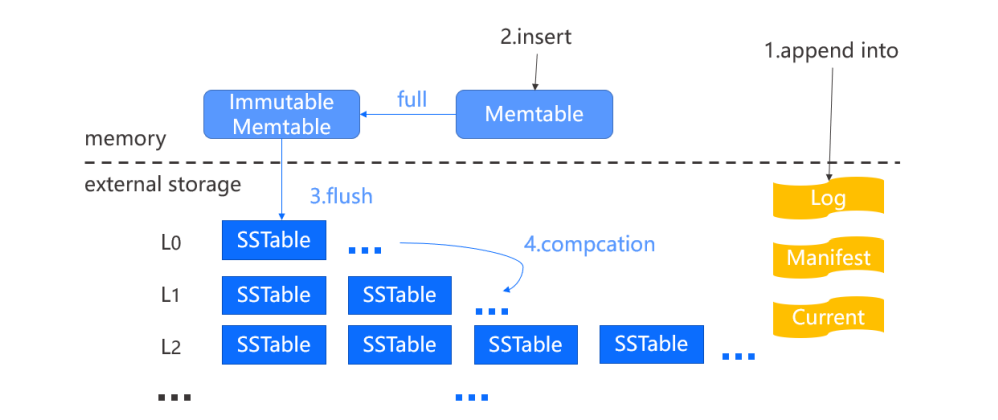
当Memtable容量达到上限时,它会转变为一个Immutable Memtable,只允许读而不允许写,并创建一个新的Memtable 提供写入。Immutable Memtable未来将转换成SSTable文件并flush到L0,为了更快速的下刷,L0的SSTable是直接生成的,因此文件之间是可能重叠的。
而随着Memtable不断的被转化成SSTable文件并写入L0后,L0的文件数量会超过容量限制,进而触发Compaction操作。
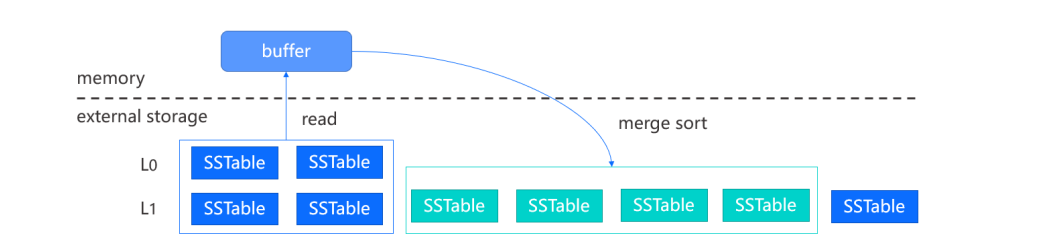
同时由于L0层有范围重叠,如上图所示,读取时从L0层读取所有文件,并在L0的下一层,即L1层找到Key范围与L0所读取文件有重叠的所有文件,然后将这些文件中的数据在内存进行合并排序后,重新生成新的SSTable文件写入L1层。由于可能有重复的新旧数据,合并过程中会删除旧数据,因此合并后一般能够减少文件的总量。其他层的合并也是类似的,只是每次只从当前层选取一个SSTable文件与下层进行合并。
Compaction操作是LSM-Tree内部数据整合的机制,也是其中最复杂的过程之一,具体实现起来有很多细节与优化方法。
对于查询来说,首先是依次在Memtable和Immutable Memtable 中查询,如果都没有找到,则在外存中继续查找。在外存中查找时,我们会从mainfest文件中读取各层中 SSTable文件的Key范围,然后找出可能包含查询Key 的 SSTable文件,这个信息一般会被缓存在内存中。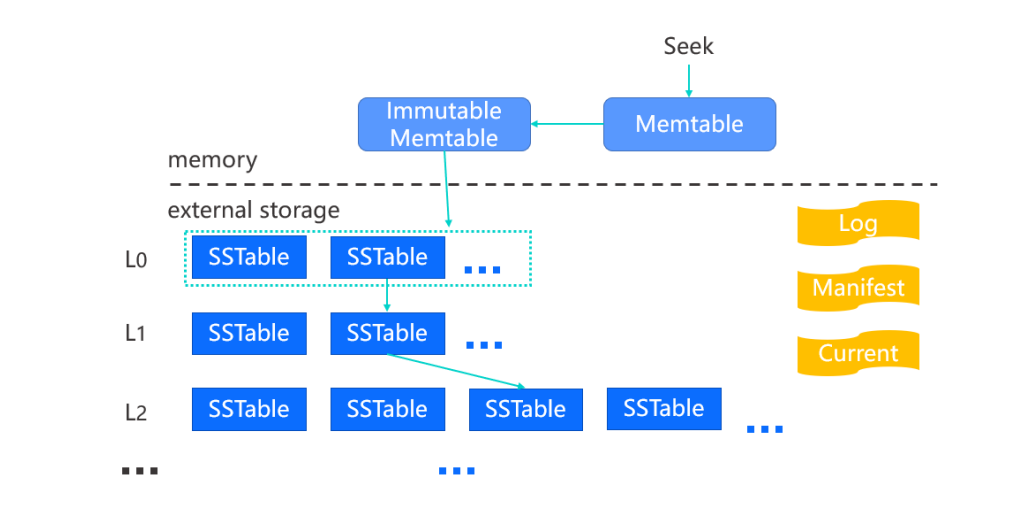
除了 L0 层外,其他各层最多只有一个 SSTable 文件可能包含查询键。也就是L0无序,除 L0 外的层都是全局有序的。随后我们将这些文件按所在层排序,位于 L0 层的在前,L0 层内的文件按时间先后逆序排列,然后按照顺序依次在SSTable 文件内查找。
SSTable 文件内的数据是排序的,并被切割成多个数据块,由内部的索引信息记录者各个数据块中 key 的范围。因此查询一般首先通过索引信息确定可能包含 Key 的数据块,然后在数据块内查找。
LevelDB 在每个 SSTable 文件中为每个数据块建立了一个布隆过滤器,在数据块内的查找前可以通过布隆过滤器来提前检验,如果确定不存在,则继续到下一个 SSTable 文件进行查找。更具体的详细实现可以看这篇LSM总结博客。
2.8LSM-Tree补充
LSM-Tree
LSM 树将离散的随机写请求都转换成批量的顺序写请求(WAL + memtable),以此提高写性能。但也带来了一些问题:
- 读放大(Read Amplification)。按照上面【读操作】的描述,读操作有可能会访问大量的文件;
- 空间放大(Space Amplification)。因为所有的写入都是顺序写(Append-only)的,不是在对数据进行直接更新(in-place update),所以过期数据不会马上被清理掉
所以维护和减少 SST 文件数量是很有必要的。
定义
- LSM树是一个横跨内存和磁盘的,包含多颗”子树”的一个森林。
- LSM树分为Level 0,Level 1,Level 2 … Level n 多颗子树,其中只有Level 0在内存中,其余Level 1-n在磁盘中。
- 内存中的Level 0子树一般采用排序树(红黑树/AVL树)、跳表或者TreeMap等这类有序的数据结构,方便后续顺序写磁盘。
- 磁盘中的Level 1-n子树,本质是数据排好序后顺序写到磁盘上的文件,只是叫做树而已。
- 每一层的子树都有一个阈值大小,达到阈值后会进行合并,合并结果写入下一层。
- 只有内存中数据允许原地更新,磁盘上数据的变更只允许追加写,不做原地更新
WAL (write-ahead log)是一种有利于顺序写的持久化日志文件。很多存储系统中都有类似的设计(如 MySQL 的 redo log/undo log、ZK 的 WAL);
RocksDB 每次写数据都会先写入 WAL 再写入 memtable,在发生故障时,通过重放 WAL 恢复内存中的数据,保证数据一致性。
这种设计有什么好处呢?这样 LSM 树就可以将有易失性(volatile)的内存看做是持久型存储,并且信任内存上的数据。
至于 WAL 的创建删除时机,每次 flush 一个 CF(列族数据) 后,都会新建一个 WAL。这并不意味着旧的 WAL 会被删除,因为别的 CF 数据可能还没有落盘,只有所有的 CF 数据都被 flush 且所有的 WAL 有关的 data 都落盘,相关的 WAL 才会被删除。
其中SSTable (sorted string table),全称是 Sorted String Table,存在于磁盘,是一个持久化的、有序的、不可更改的 Map 结构,Key 和 Value 都是任意的 Byte 串。上文提到内存中的 memtable 在满足条件的情况下会执行 flush 操作,SSTable 的 文件结构如下: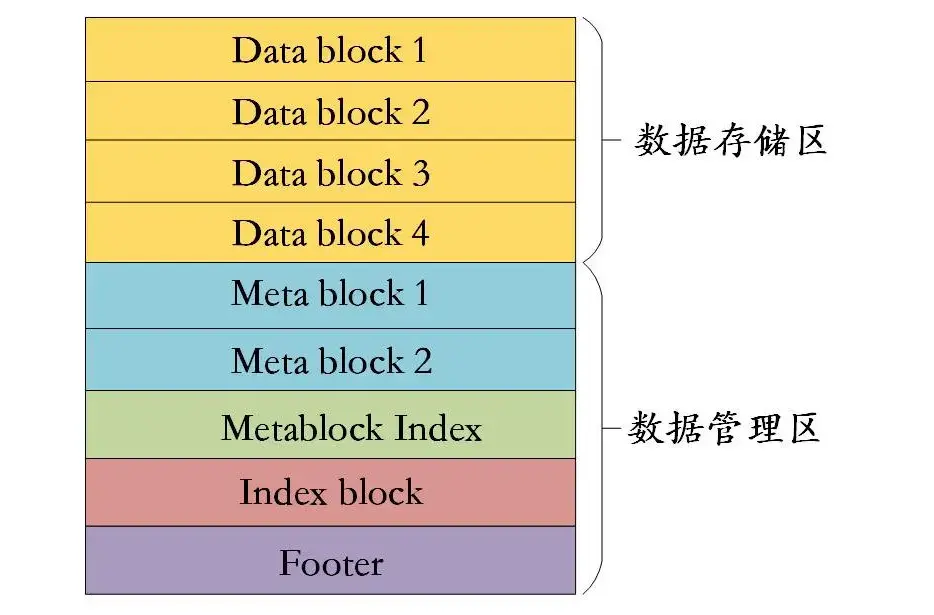
- 数据块 Data Block,存储有序键值对,是 SSTable 的数据实体;为了节省存储空间,并不会为每一对 key-value 对都存储完整的 key 值,而是存储与上一个 key 非共享的部分,避免了 key 重复内容的存储(这种通过 delta encode 的方式节省空间的方式在其他存储中间件底层中也很常见)。
- Meta Block,存储 Filter 相关信息,用于加快 sst 中查询数据的效率;Filter 通过 Bloom Filter 来过滤判断指定的 data block 中是否存在要查询的数据。
- Meta Index Block,对 Meta Block 的索引,它只有一条记录,key 是 meta index 的名字(也就是 Filter 的名字),value 为指向 meta index 的位置;
- Index Block,index block 用来存储所有 data block 的相关索引信息。indexblock 包含若干条记录,每一条记录代表一个 data block 的索引信息;
- Footer,指向各个分区的位置和大小。Footer 是定长的,读取 SSTable 文件的时候,就是从文件末尾,固定读取字节数,进而得到了 Footer 信息。 Footer 中的信息,指明了 MetaIndexBlock 和 IndexBlock 的位置,进而找到 MetaBlock 和 DataBlock。****
读&写

- 在 active memtable 中查找;
- 如果 active memtable 没有,则在 immutable memtable 中查找;
- 如果 immutable memtable 没有,则在 L0 SSTable 中查找(RocksDB 采用遍历的方法查找 L0 SSTable,为了提高查找效率会控制 L0 文件的个数);
- 如果找不到,则在剩余的 SSTable 中查找(对于 L1 层以及 L1 层以上层级的文件,每个 SSTable 没有交叠,可以使用二分查找快速找到 key 所在的 Level 以及 SSTable)
每个 SSTable 在查找之前通过 bloom filter 快速判断数据是否存在于当前文件,减少不必要的 IO。 RocksDB 为 SST 中访问频繁的 data blocks 设置了一个读缓存结构 Block cache,并提供了两种开箱即用的实现 LRUCache 和 ClockCache 。
- 写操作会先写 WAL 文件,保证数据不丢失;
- 完成 WAL 写入后,将数据写入到 内存中的 active memtable 中(为了保证有序性,RocksDB 使用跳表数据结构实现 memtable);
- 然后等 memtable 数据达到一定规模时,会转变成 immutable memtable,同时生成新的 memtable 提供服务;
- 在满足落盘条件后,immutable memtable 会被合并刷入到硬盘的 SST 中;
顺带一提,默认情况下 RocksDB 中的写磁盘行为都是异步写,仅仅把数据写进了操作系统的缓存区就返回了(pageCache),而这些数据被写进磁盘是一个异步的过程。异步写的吞吐率是同步写的一千多倍。异步写的缺点是机器或者操作系统崩溃时可能丢掉最近一批写请求发出的由操作系统缓存的数据,但是 RocksDB 自身崩溃并不会导致数据丢失。而机器或者操作系统崩溃的概率比较低,所以大部分情况下可以认为异步写是安全的。
LSM 树设计思想总结
LSM 树将对磁盘的随机写入转化为了磁盘友好型的顺序写(无论机械磁盘还是 SSD,随机读写都要远远慢于顺序读写),从而大大提高了写性能。
那么是怎么转化的呢?核心就是在内存中维护一个有序的内存表(memtable),当内存表大于阈值的时候批量刷入磁盘,生成最新的 SSTable 文件。因为本身 memtable 已经维护了按键排序的键值对,所以这个步骤可以高效地完成。
写入内存表时先将数据写入 WAL 日志,用以在发生故障时,通过重放 WAL 恢复内存中的数据,保证数据库的数据一致性。
在这种追加(Append-only)写入模式下,删除数据变成了对数据添加删除标记,更新数据变成了写入新的 value,在同一个时间数据库中会存在同个 key 的新值和旧值。这种影响被称之为 空间放大(Space Amplification)。随着数据的写入,底层的 SSTable 文件也会越来越多。
读请求在这个模式下,变成了先在内存中寻找关键字,如果找不到则在磁盘中按照新-> 旧查找 SSTable 文件。为了优化这种访问模式的读性能,存储引擎通常使用常见的针对读的优化策略,比如使用额外的 Bloom Filter、读 Cache。
这种需要多次读取的过程(或者说影响)被称之为读放大(Read Amplification)。很显然,读放大会影响 LSM 树的读性能。为了优化读性能(读放大),同时优化存储空间(空间放大),LSM 树通过在运行合并和压缩过程减少 SSTable 文件数量,删除无效(被删除或者被覆盖) 的旧值。这一过程被称之为 compaction。
但是 compaction 也会一些影响,在数据库的生命周期中每次的数据写入实际上会造成多次的磁盘写入。这种影响被称之为写放大(Write Amplification)。在写入繁重的应用程序中,性能瓶颈可能是数据库可以写入磁盘的速度。在这种情况下,写放大会导致直接的性能代价:存储引擎写入磁盘的次数越多,可用磁盘带宽内的每秒写入次数越少。
这也是我认为 LSM 引擎存储的一个缺点,就是压缩过程有可能会干扰到正在进行的读写请求。尽管存储引擎尝试逐步执行压缩而不影响并发访问,但是磁盘资源有限,所以很容易发生请求需要等待磁盘完成昂贵的压缩操作。对吞吐量和平均响应时间的影响通常很小,但是如果是高百分位情况下,有时就会出现查询响应较长的情况。
具体提到的 RocksDB 实现中,写放大、读放大、空间放大,这三者就像 CAP 定理一样,无法同时达到最优。为此 RocksDB 暴露了很多参数来让使用者进行调优,以适应更多的应用场景。这其中很大一部分工作是在写放大、读放大和空间放大这三个放大因子之间做好 trade off。
2.9LSM 树 vs B+ 树
2.9.1设计理念不同
虽然像 LSM 树一样,B+ 树保持按键排序的键值对(这允许高效的键值查找和范围查询),但是两者设计理念完全不同。
- LSM 树将数据库分解为可变大小的段,通常是几兆字节或更大的大小,并且总是按顺序编写段。
- 相比之下,B+ 树将数据库分解成固定大小的块或页面,传统上大小为 4KB(有时会更大),并且一次只能读取或写入一个页面。这种设计更接近于底层硬件,因为磁盘也被安排在固定大小的块中。
2.9.2数据的更新和删除方面
- B+树可以做到原地更新和删除(in-place update),这种方式对数据库事务支持更加友好,因为一个 key 只会出现一个 Page 页里面;
- 但由于 LSM 树只能追加写(out-place update),并且在 L0 层的 SSTable 中会重叠,所以对事务支持较弱,只能在 compaction 的时候进行真正地更新和删除。
2.9.3性能方面
- LSM 树的优点是支持高吞吐的写(可认为是 O(1)),这个特点在分布式系统上更为看重,当然针对读取普通的 LSM 树结构,读取是 O(n) 的复杂度,在使用索引或者缓存优化后的也可以达到 O(logN)的复杂度。
- B+ 树的优点是支持高效的读(稳定的 O(logN)),但是在大规模的写请求下(复杂度 O(LogN)),效率会变得比较低,因为随着 insert 的操作,为了维护树结构,节点会不断的分裂和合并。操作磁盘的随机读写概率会变大,故导致性能降低。
通常来说,我们会说,LSM 树写性能会优于 B 树,而 B 树的读性能会优于 LSM 树。但是请不要忽略 LSM 树写放大的影响,在进行性能判定是要更辩证的思考。
第三章 查询处理
3.1查询处理概述
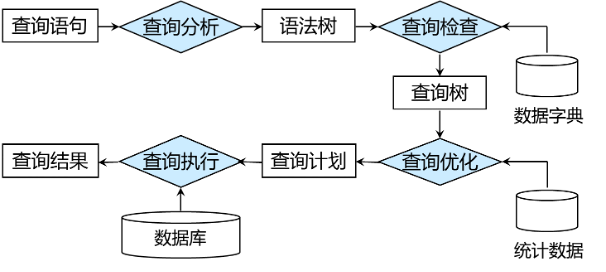
关系数据库管理系统查询处理可以分为4个阶段:查询分析、查询检查、查询优化和查询执行。
- 查询分析 :对用户提交的查询语句进行扫描、词法分析和语法分析,判断是否符合SQL语法规则,若没有语法错误,就会生成一棵语法树。
- 查询检查 :对语法树进行查询检查,首先根据数据字典中的模式信息检查语句中的数据对象,如关系名、属性名是否存在和有效;还要根据数据字典中的用户权限和完整性约束信息对用户的存取权限进行检查。若通过检查,则将数据库对象的外部名称转换成内部表示。这个过程实际上是对语法树进行语义解析的过程,最后语法树被解析为一个具有特定语义的关系代数表达式,其表示形式仍然是一棵树,称为查询树。
- 查询优化 :每个查询都会有多种可供选择的执行策略和操作算法,查询优化就是选择一个能高效执行的查询处理策略。一般将查询优化分为代数优化和物理优化。代数优化指对关系代数表达式进行等价变换,改变代数表达式中操作的次序和组合,使查询执行更高效;物理优化则是指存取路径和底层操作算法的选择,选择依据可以是基于规则、代价、语义的。查询优化之后,形成查询计划。
- 查询执行 :查询计划由一系列操作符构成,每一个操作符实现计划中的一步。查询执行阶段,系统将按照查询计划逐步执行相应的操作序列,得到最终的查询结果。
3.2 选择运算
选择操作的典型实现方法有全表扫描法和索引扫描法。
3.2.1 全表扫描法
对查询的基本表顺序扫描,逐一检查每个元组是否满足选择条件,把满足条件的元组作为结果输出。
假设可以使用的内存为M块,全表扫描的算法思想如下:
- 按物理次序读表T的M块到内存;
- 检查内存的每个元组t,如果t满足选择条件,则输出t;
- 如果表T还有其他块未被处理,重复(1)和(2)。
这种方法适合小表,对规模大的表要进行顺序扫描,当选择率(即满足条件的元组数占全表比例)较低时,此算法效率很低。
3.2.2 索引扫描法
当选择条件中的属性上有索引(例如B+树索引或Hash索引)时,通过索引先找到满足条件的元组指针,再通过元组指针直接在要查询的表中找到元组。
[例1 ] 等值查询:select * from t1 where col=常量,并且col上有索引(B+树索引或Hash索引均可) ,则使用索引得到col为该常量元组的指针,通过元组指针在表t1中检索到结果。
[例2 ] 范围查询: select * from t1 where col > 常量,并且col上有B+树索引,使用B+树索引找到col=常量的索引项,以此为入口点在B+树的顺序集上得到col > 常量的所有元组指针, 通过这些元组指针到t1表中检索满足条件的元组。
[例 3 ] 合取条件查询:select * from t1 where col1=常量a AND col2 >常量b,如果 col1和 col1上有组合索引(col1,col2),则利用此组合索引进行查询筛选;否则,如果 col1和 col2上分别有索引,则:
方法一:分别利用各自索引查找到满足部分条件的一组元组指针,求这2组指针的交集,再到t1表中检索得到结果。
方法二:只利用索引查找到满足该部分条件的一组元组指针,通过这些元组指针到t1表中检索,对得到的元组检查另一些选择条件是否满足,把满足条件的元组作为结果输出。
一般情况下,当选择率较低时,基于索引的选择算法要优于全表扫描。但在某些情况下,如选择率较高、或者要查找的元组均匀分散在表中,这时索引扫描法的性能可能还不如全表扫描法,因为还需要考虑扫描索引带来的额外开销。
3.3 排序运算
排序是数据库中的一个基本功能,用户通过Order by子句即能达到将指定的结果集排序的目的,而且不仅仅是Order by子句,Group by、Distinct等子句都会隐含使用排序操作。
3.3.1 利用索引避免排序
为了优化查询语句的排序性能,最好的情况是避免排序,合理利用索引是一个不错的方法。因为一些索引本身也是有序的,如B+树,如果在需要排序的字段上面建立了合适的索引,那么就可以跳过排序过程,提高查询速度。
例如:假设t1表存在B+树索引key1(key_part1, key_part2),则以下查询可以利用索引来避免排序:
SELECT * FROM t1 ORDER BY key_part1, key_part2;
SELECT * FROM t1 WHERE key_part1 = constant ORDER BY key_part2;
SELECT * FROM t1 WHERE key_part1 > constant ORDER BY key_part1;
SELECT * FROM t1 WHERE key_part1 = constant1 AND key_part2 > constant2 ORDER BY key_part2;如果排序字段不在索引中,或者分别存在于多个索引中,或者排序键的字段顺序与组合索引中的字段顺序不一致,则无法利用索引来避免排序。
3.3.2 数据库内部排序方法
对于不能利用索引来避免排序的查询,DBMS必须自己实现排序功能以满足用户需求。实现排序的算法可以是文件排序,也可以是内存排序,具体要由排序缓冲区(sort buffer)的大小和结果集的大小来确定。
数据库内部排序的实现主要涉及3种经典排序算法:快速排序、归并排序和堆排序。对于不能全部放在内存中的关系,需要引入外排序,最常用的就是外部归并排序。外部归并排序分为两个阶段:Phase1 – Sorting,对主存中的数据块进行排序,然后将排序后的数据块写回磁盘;Phase2 – Merging,将已排序的子文件合并成一个较大的文件。
3.3.2.1 常规排序法
一般情况下通用的常规排序方法如下:
- (1) 从表t中获取满足WHERE条件的记录;
- (2) 对于每条记录,将记录的主键+排序键(id,colp)取出放入sort buffer;
- (3) 如果sort buffer可以存放所有满足条件的(id,colp)对,则进行排序;否则sort buffer满后,进行排序并固化到临时文件中。(排序算法采用快速排序);
- (4) 若排序中产生了临时文件,需要利用归并排序算法,保证临时文件中记录是有序的;
- (5) 循环执行上述过程,直到所有满足条件的记录全部参与排序;
- (6) 扫描排好序的(id,colp)对,并利用id去取SELECT需要返回的目标列;
- (7) 将获取的结果集返回给用户。
从上述流程来看,是否使用文件排序主要看sort buffer是否能容下需要排序的(id,colp)对。此外一次排序涉及两次I/O:第一次是取(id,colp),第二次是取目标列。由于第一次返回的结果集是按colp排序,因此id是乱序的。通过乱序的id去取目标列时,会产生大量的随机I/O。因此,可以考虑对第二次I/O进行优化,即在取数据之前首先将id排序并放入缓冲区,然后按id顺序去取记录,从而将随机I/O转为顺序I/O。
为了避免第二次I/O,还可以考虑一次性取出(id,colp,目标列),当然这样对缓冲区的需求会更大。
3.3.2.2 堆排序法
堆排序法适用于形如”order by limit m,n”的这类排序问题,即跳过m条数据,提取n条数据。这种情况下,虽然仍然需要所有元组参与排序,但是只需要m+n个元组的sort buffer空间即可,对于m和n很小的场景,基本不会出现因sort buffer不够而需要使用临时文件进行归并排序的问题。对于升序,采用大顶堆,最终堆中的元素组成了最小的n个元素;对于降序,则采用小顶堆,最终堆中的元素组成了最大的n的元素。
3.4 连接运算
连接操作是查询处理中最常用最耗时的操作之一。主要有4种实现方法:嵌套循环、排序-合并、索引连接和散列连接。
首先引入2个术语:外关系(outer relation)和内关系(inner relation)。外关系是左侧数据集,内关系是右侧数据集。例如:对于A JOIN B,A为外关系,B为内关系。多数情况下,A JOIN B 的成本跟 B JOIN A 的成本是不同的。假定外关系有m个元组,占M个页,内关系有n个元组,占N个页。
3.4.1 嵌套循环连接
嵌套循环连接是最简单且通用的连接算法,其执行步骤为:针对外关系的每一行,查看内关系里的所有行来寻找匹配的行。这是一个双重循环,时间复杂度为O(n*m)。
在磁盘 I/O 方面, 针对外关系的每一行,内部循环需要从内关系读取m行。这个算法需要从磁盘读取 n+ n*m 行。但是,如果外关系足够小,我们可以把它先读入内存,那么就只需要读取 n+m 行。按照这个思路,外关系就应该选更小的那个关系,因为它有更大的机会装入内存。
当然,内关系如果可以由索引代替,对磁盘 I/O 将更有利。
当外关系太大无法装入内存时,采用块嵌套循环连接方式,对磁盘 I/O 更加有利。其基本思路是将逐行读取数据,改为以页(块)为单位读取数据。算法如下:
- (1) 从磁盘读取外关系的一个数据页到内存;
- (2) 从磁盘依次读取内关系的所有数据页到内存,与内存中外关系的数据进行比较,保留匹配的结果;
- (3) 从磁盘读取外关系的下一个数据页,并继续执行(2),直至外关系的最后一个页面。
与嵌套循环连接算法相比,块嵌套循环连接算法的时间复杂度没有变化,但降低了磁盘访问开销,变为M+M*N。其中,M为外关系的页数,N为内关系的页数。
3.4.2 索引嵌套循环连接
在嵌套循环连接中,若在内关系的连接属性上有索引,则可以用索引查找替代文件扫描。对于外关系的每一个元组,可以利用索引查找内关系中与该元组满足连接条件的元组。这种连接方法称为索引嵌套循环连接,它可以在已有索引或者为了计算该连接而专门建立临时索引的情况下使用。
索引嵌套循环连接的代价可以如下计算。对于外关系的每一个元组,需要先在内关系的索引上进行查找,再检索相关元组。在最坏的情况下,缓冲区只能容纳外关系的一页和索引的一页。此时,读取外关系需M次I/O操作,这里的M指外关系的数据页数;对于外关系中的每个元组,在内关系上进行索引查找,假设索引查找带来的I/O开销为C,则总的I/O开销为:M+(m×C),其中m为外关系的元组数。
这个代价计算公式表明,如果两个关系上均有索引时, 一般把元组较少的关系作外关系时效果较好。
3.4.3 排序-合并连接
排序-合并连接算法常用于等值连接,尤其适合参与连接的表已经排好序的情况。其方法如下:
第一步:如果参与连接的表没有排好序,则根据连接属性排序;
第二步:sorted_merge:
- (1) 初始化两个指针,分别指向两个关系的第一个元组;
- (2) 比较两个关系的当前元组(当前元组=指针指向的元组);
- (3) 如果匹配,保留匹配的结果,两个指针均后移一个位置;
- (4) 如果不匹配,就将指向较小元组的那个指针后移一个位置;
- (5) 重复步骤(2)、(3)、(4),直到其中一个关系的指针移动到末尾。
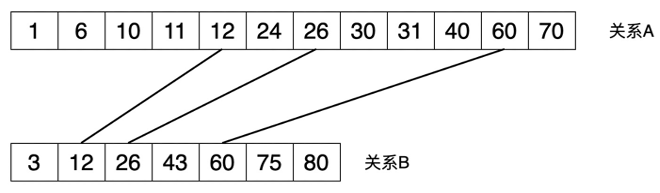
因为两个关系都是已排序的,不需要”回头去找”,所以此方法的时间复杂度为O(n+m)。如果两个关系还需要排序,则还要考虑排序的成本:O(n*Log(n) + m*Log(m))。
很多情况下,参与连接的数据集已经排好序了,比如:表内部就是有序的,或者参与连接的是查询中已经排好序的中间结果,那么选用排序-合并算法是比较合适的。
3.4.4 散列连接
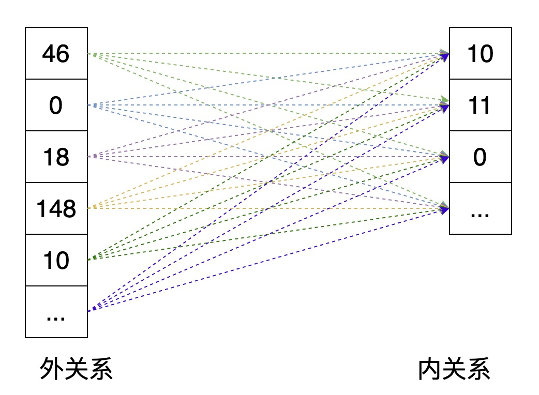
散列连接算法也是适用于等值连接的算法。
散列连接分成两个阶段:第一步,划分阶段,为较小的关系建立hash表,将连接属性作为hash码;第二步,试探阶段,对另一张表的连接属性用同样的hash函数进行散列,将其与相应桶中匹配的元组连接起来。
本算法要求内存足够大,小表的hash表如果能全部放进内存,则效果较好。
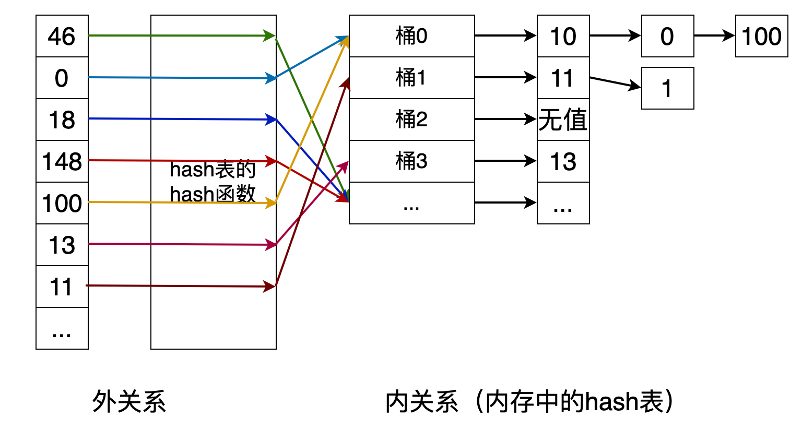
在时间复杂度方面需要做些假设来简化问题:
- (1) 内关系被划分成 X 个散列桶。散列函数几乎均匀地分布每个关系内数据的散列值,即散列桶大小一致。
- (2) 外关系的元素与散列桶内所有元素的匹配,成本是散列桶内元素的数量。
算法的开销包括创建散列表的成本(m) +散列函数的计算开销 * n + (m/X) * n。如果散列函数创建的散列桶的规模足够小,则算法复杂度为O(m+n)。
3.4.5 连接算法的选择
具体情况下,应该选择以上哪种连接算法,有许多因素要考量:
- (1) 空闲内存:没有足够的内存就无法使用内存中的散列连接。
- (2) 两个数据集的大小。比如,如果一个大表连接一个很小的表,那么嵌套循环连接就比散列连接快,因为后者有创建散列表的高昂成本;如果两个表都非常大,那么嵌套循环连接的CPU成本就很高。
- (3) 是否有索引:如果连接属性上有两个B+树索引的话,合并连接会是很好的选择。
- (4) 关系是否已经排序:这时候合并连接是最好的选择。
- (5) 结果是否需要排序:即使参与连接的是未排序的数据集,也可以考虑使用成本较高的合并连接(带排序的),比如得到排序的结果后,我们还可以将它用于另一个合并联接,或者查询中存在ORDER BY/GROUP BY/DISTINCT等操作符,它们隐式或显式地要求一个排序结果。
- (6) 连接的类型:是等值连接?还是内连接?外连接?笛卡尔积?或者自连接?有些连接算法在某些情况下是不适用的。
- (7) 数据的分布:如果连接条件的数据是倾斜的,用散列连接不是好的选择,因为散列函数将产生分布极不均匀的散列桶。
- (8) 多表连接:连接顺序的选择很重要。
另外,还可能考虑实现方式问题,比如连接操作使用多线程或多进程的代价考量。因此,DBMS需要通过查询优化器来选择恰当的执行计划。
3.5 表达式计算
如何计算包含多个运算步骤的关系代数表达式?有两种方法:物化计算和流水线计算。
3.5.1 物化计算
物化计算以适当的顺序每次执行一次操作;每次计算的结果被物化到一个临时关系以备后用。其缺点为:需要构造临时关系,而且这些临时关系必须写到磁盘上(除非很小)。
表达式的执行顺序可以依据表达式在查询树中的层次而定,从树的底部开始。
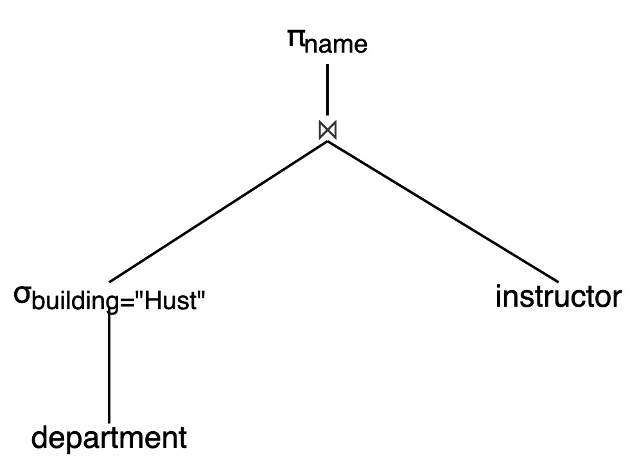
如图所示,此例中只有一个底层运算:department上的选择运算,底层运算的输入是数据库中的关系department。用前面提到的算法执行树中的运算,并将结果存储在临时关系中。在树的高一层中,使用这个临时关系来进行计算,这时输入的要么是临时关系,要么是一个数据库关系。通过重复这一过程,最终可以计算位于树的根节点的运算,从而得到表达式的最终结果。
由于运算的每个中间结果会被物化用于下一层的运算,此方法称为物化计算。物化计算的代价不仅是那些所涉及的运算代价的总和,还可能包括将中间结果写到磁盘的代价。
3.5.2 流水线计算
流水线计算可同时计算多个运算,运算的结果传递给下一个,而不必保存临时关系。这种方法通过减少查询执行中产生的临时文件的数量,来提高查询执行的效率。
比如在上一章里面,可以将选择、连接操作和投影操作组合起来,放入一条流水线,选择得到一个结果传给连接、连接产生一个结果元组马上传送给投影操作去做处理,避免中间结果的创建,从而直接产生最终结果。
创建一个操作的流水线可以带来的好处是:
- (1) 消除读和写临时关系的代价,从而减少查询计算代价。
- (2) 流水线产生查询结果,边生成边输出给用户,提高响应时间。
流水线可按两种方式来执行:
- 方式一:需求驱动方式,在操作树的顶端的将数据往上拉。
- 方式二:生产者驱动方式,将数据从操作树的底层往上推。
需求驱动的流水线方法比生产者驱动的流水线方法使用更广泛,因为它更容易实现。但流水线技术限制了能实现操作的可用算法。例如,若连接运算的左端输入来自流水线,则不能使用排序-合并连接,但可以用索引连接算法。由于这些限制,并非所有情况下流水线方法的代价都小于物化方法。
第四章 查询优化
4.1 查询优化概述
查询优化即求解给定查询语句的高效执行计划的过程。它既是关系数据库管理系统实现的关键技术,又是关系系统的优点所在。由DBMS进行查询优化的好处在于:查询优化的优点不仅在于用户不必考虑如何最好的表达查询以获得较高的效率,而且在于系统可以比用户程序的”优化”做得更好。
查询计划,从形式上看是一颗二叉树,树叶是每个单表对象,两个树叶的父节点是一个连接操作符连接后的中间结果(另外还有一些其他节点如排序等也可以作为中间结果),这个结果是一个临时关系,这样直至根节点。
从一个查询计划看,涉及的主要”关系节点”包括:
- 单表节点:考虑单表的获取方式(全表扫描,或索引获取,或索引定位再I/O到数据块获取数据)。这是一个物理存储到内存解析成逻辑字段的过程。
- 两表节点:考虑两表以何种方式连接,代价有多大,连接路径有哪些等。表示内存中的元组如何进行元组间的连接。此时,元组通常已经存在于内存中。这是一个完整用户语义的逻辑操作,但只是局部操作,只涉及两个具体的关系。完成用户全部语义,需要配合多表的连接顺序的操作。
- 多表中间节点:考虑多表连接顺序如何构成代价最少的”执行计划”。决定连接执行的顺序。
查询优化的总目标是选择有效的策略,求得给定关系表达式的值,使得查询代价较小。因为查询优化的搜索空间有时非常大,实际系统选择的策略不一定是最优的,而是较优的。
查询优化主要包括逻辑优化和物理优化。其中,逻辑优化又可包含语法级查询优化、基于规则的优化等;而物理优化主要指基于代价的优化。语法级优化是基于语法的等价转换;基于规则的优化(如依据关系代数的规则或依据经验的规则等)具有操作简单且能快速确定执行方式的优点,但这种方法只是排除了一部分不好的可能;基于代价的优化是在查询计划生成过程中,计算每条存取路径进行量化比较,从而得到开销最小的情况,但如果组合情况多则开销的判断时间就很多。查询优化器的实现,多是这两种优化策略的组合使用。
4.2 逻辑优化
查询优化器在逻辑优化阶段主要解决的问题是:如何找出SQL语句的等价变换形式,使SQL执行更高效。
4.2.1代数优化
代数优化是基于关系代数等价变换规则的优化方法。
代数优化策略是通过对关系代数表达式的等价变换来提高查询效率。所谓关系代数表达式的等价是指用相同的关系代替两个表达式中相应的关系所得到的结果是相同的。两个关系表达式E1和E2是等价的。
4.2.1.1 关系代数表达式等价变换规则
常用的关系代数等价变换规则如下:
- 连接、笛卡尔积的交换律
设E1和E2为关系代数表达式,F为连接运算条件,则有:
E1×E2 ≡ E2×E1
E1⋈E2 ≡ E2⋈E1
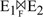 ≡
≡ 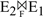
对于连接和笛卡尔积运算,可以交换前后位置,其结果不变。例如,两表连接算法中有嵌套循环连接算法,对外表和内表有要求,外表尽可能小则有利于做”基于块的嵌套循环连接”,所以通过交换律可以将元组少的表作为外表。
- 连接、笛卡尔积结合律
设E1、E2、E3为关系代数表达式,F1、F2为连接运算条件。则有:
(E1×E2)×E3 ≡ E1×(E2×E3)
(E1⋈E2)⋈E3 ≡ E1⋈(E2⋈E3)
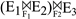 ≡
≡ 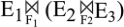
对于连接、笛卡尔积运算,如果新的结合有利于减少中间关系的大小,则可以优先处理。
- 投影的串接定律
设E为关系代数表达式,Ai(i=1,2,3,…,n),Bj(j=1,2,3,…,m)是属性名,且{A1,A2,…,An}为{B1,B2,…,Bm}的子集。则有:
∏A1,A2,…,An(∏B1,B2,…,Bm(E)) ≡ ∏A1,A2,…,An (E)
在同一个关系上,只需做一次投影运算,且一次投影时选择多列同时完成。所以许多数据库优化引擎会为一个关系收集齐该关系上的所有列,即目标列和WHERE、GROUP BY等子句中涉及到的所有该关系的列。
- 选择的串接律
设E为关系代数表达式,F1、F2为选择条件。则有:
σF1(σF2(E)) ≡ σF1∧F2(E)
此变换规则对于优化的意义在于:选择条件可以合并,使得一次选择运算就可检查全部条件,而不必多次过滤元组,所以可以把同层的合取条件收集在一起,统一进行判断。
- 选择和投影的交换律
设E为关系代数表达式,F为选择条件,Ai(i=1,2,3,…,n)是属性名。选择条件F只涉及属性A1,A2,…,An。则有:
σF(∏A1,A2,…,An (E)) ≡∏A1,A2,…,An(σF(E))
此变换规则对于优化的意义在于:先投影后选择可以改为先选择后投影,这对于以行为单位来存储关系的主流数据库而言,很有优化意义。按照这种存储方式,系统总是先获取元组,然后才能解析得到其中的列。
设E为关系代数表达式,F为选择条件,Ai(i=1,2,3…,n)是属性名,选择条件F中有不属于A1,A2,…,An的属性B1,B2,…,Bn。则有:
∏A1,A2,…,An(σF(E)) ≡ ∏A1,A2,…,An(σF(∏A1,A2,…,An,B1,B2,…,Bm(E)))
此变换规则对于优化的意义在于:先选择后投影可以改为先做带有选择条件中的列的投影,然后选择,最后再完成最外层的投影。这样内层的选择和投影可以同时进行,不会增加过多的计算开销,但能减小中间结果集的规模。
- 选择与笛卡尔积的交换律
设E1、E2为关系代数表达式,F为选择条件,F中涉及的属性都是E1中的属性,则有:
σF(E1×E2) ≡ σF(E1)×E2
如果F=F1∧F2,且F1只涉及E1中的属性,F2只涉及E2中的属性,则有:
σF(E1×E2) ≡ σF1(E1)×σF2(E2)
此变换规则对于优化的意义在于:条件下推到相关的关系上,先做选择后做笛卡尔积运算,这样可以减小中间结果的大小。
- 选择与并的分配律
如果E1和E2有相同的属性名,且E= E1∪E2,则有:
σF(E1∪E2) ≡ σF(E1) ∪σF (E2)
此变换规则对于优化的意义在于:条件下推到相关的关系上,先选择后做并运算,可以减小每个关系输出结果的大小。
- 选择与差的分配律
如果E1和E2有相同的属性名,则:
σF(E1-E2) ≡ σF(E1)-σF(E2)
此变换规则对于优化的意义在于:条件下推到相关的关系上,先选择后做差运算,可以减小每个关系输出结果的大小。
- 投影与笛卡尔积的交换律
设A1,A2,…,An是E1的属性,B1,B2,…,Bm是E2的属性,则有:
∏A1,A2,…,An,B1,B2,…,Bm(E1×E2) ≡ ∏A1,A2,…,An(E1)×∏B1,B2,…,Bm(E2)
此变换规则对于优化的意义在于:先投影后做笛卡尔积,可减少做笛卡尔积前每个元组的长度,使得计算后得到的新元组的长度也变短。
- 投影与并的交换律
如果E1和E2有相同的属性名,则有:
∏A1,A2,…,An (E1∪E2) ≡ ∏A1,A2,…,An (E1)∪∏A1,A2,…,An (E2)
此变换规则对于优化的意义在于:先投影后做并运算,可减少做并运算前每个元组的长度。
4.2.1.2 针对不同运算符的优化规则
针对不同运算符的优化规则如表所示。
运算符主导的优化: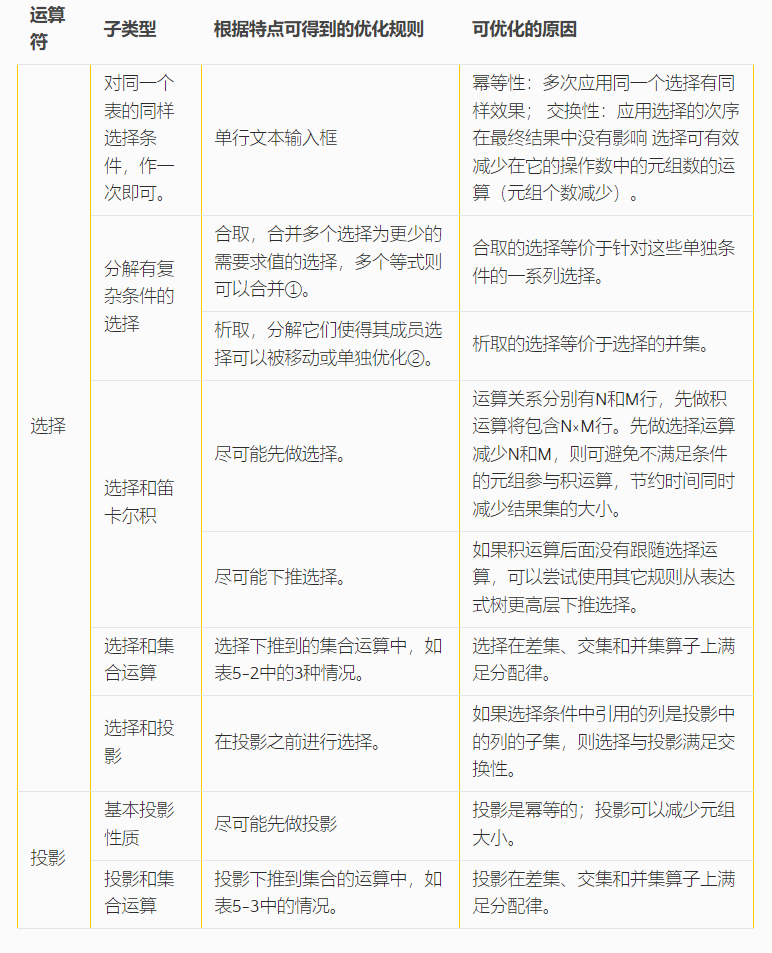
- 如WHERE A.a=B.b AND B.b=C.c可以合并为={A.a,B.b,C.c}而不是两个等式={A.a,B.b}和={B.b,C.c}。
- 如WHERE A.a=3 OR A.b>8,如果A.a、A.b列上分别有索引,也许SELECT * FROM A WHERE A.a=3 UNION SELECT * FROM A WHERE A.b>8可以分别利用各自的索引提高查询效率。
选择下推到集合的运算
| 初始式 | 优化后的等价表达式 | ||
|---|---|---|---|
| 等价表达式一 | 等价表达式二 | 等价表达式三 | |
| σA(R-S) | σA(R)-σA(S) | σA(R)-S | |
| σA(R∪S) | σA(R)∪σA(S) | ||
| σA(R∩S) | σA(R)∩σA (S) | σA(R)∩S | R∩σA(S) |
投影下推到集合的运算
| 初始式 | 优化后的等价表达式 |
|---|---|
| ∏A1,A2,…,An(R-S) | ∏A1,A2,…,An(R)- ∏A1,A2,…,An(S) |
| ∏A1,A2,…,An(R∪S) | ∏A1,A2,…,An(R) ∪∏A1,A2,…,An(S) |
| ∏A1,A2,…,An(R∩S) | ∏A1,A2,…,An(R) ∩∏A1,A2,…,An(S) |
4.2.1.3 查询树启发式规则
包括:
- 选择运算应尽可能先做。
- 把投影运算和选择运算同时进行。如有若干投影和选择运算,并且它们都对同一个关系操作,则可以在扫描次关系的同时完成所有这些运算以避免重复扫描关系。
- 把投影同其前或后的双目运算结合起来,没有必要为了去掉某些字段而扫描一遍关系。
- 把某些选择同在它前面要执行的笛卡尔积结合起来称为一个连接运算。连接(特别是等值连接)运算比笛卡尔积性能高很多。
- 找出公共子表达式,将其计算结果缓存起来,避免重复计算。
4.2.2 语法级查询优化
语法级优化要解决的主要问题是找出SQL语句的等价变换形式,使得SQL执行更高效,包括:
- 子句局部优化。如等价谓词重写、where和having条件简化等。
- 关联优化。如子查询优化、连接消除、视图重写等。
- 形式变化优化。如嵌套连接消除等。
以下介绍几种常见的优化方法。
4.2.2.1 子查询优化
早期的查询优化器对子查询都采用嵌套执行的方式,即对父查询中的每一行都执行一次子查询,这样效率很低,因此对其进行优化很有必要。例如,将子查询转为连接操作之后,有如下好处:
- 子查询不用多次执行;
- 优化器可以根据统计信息来选择不同的连接方法和不同的连接顺序;
- 子查询中的连接条件、过滤条件分别变成了父查询的连接条件和过滤条件,优化器可以对这些条件进行下推,以提高执行效率。
- 常见子查询优化技术
(1) 子查询合并
在语义等价条件下,多个子查询可以合并成一个子查询,这样多次表扫描,多次连接减少为单次表扫描和单次连接。例如:
SELECT *
FROM t1
WHERE a1<10 AND (
EXISTS (SELECT a2 FROM t2 WHERE t2.a2<5 AND t2.b2=1) OR
EXISTS (SELECT a2 FROM t2 WHERE t2.a2<5 AND t2.b2=2)
);可优化为:
SELECT *
FROM t1
WHERE a1<10 AND (
EXISTS (SELECT a2 FROM t2 WHERE t2.a2<5 AND (t2.b2=1 OR t2.b2=2)
);此例中,两个EXISTS子查询合并为一个子查询,查询条件也进行了合并。
(2) 子查询展开
子查询展开又称子查询反嵌套,子查询上拉。实质是把某些子查询重写为等价的多表连接操作。带来好处是,有关的访问路径、连接方法和连接顺序可能被有效使用,使得查询语句的层次尽可能地减少。常见的IN / ANY / SOME / ALL / EXISTS依据情况转为半连接(SEMI JOIN)。例如:
SELECT *
FROM t1, (SELECT * FROM t2 WHERE t2.a2>10) v_t2
WHERE t1.a1<10 AND v_t2.a2<20;可优化为:
SELECT *
FROM t1, t2
WHERE t1.a1<10 AND t2.a2<20 AND t2.a2>10;此例中,原本的子查询变为了t1、t2表的连接操作,相当于把t2表从子查询中上拉了一层。
子查询展开是一种最常用的子查询优化技术,如果子查询是只包含选择、投影、连接操作的简单语句,没有聚集函数或者group子句,则可以上拉,前提是上拉后的结果不能带来多余元组,需遵循以下规则:
- 如果上层查询结果没有重复(select包含主键),则可以展开子查询,并且展开后的查询的select子句前应加上distinct标志;
- 如果上层查询的select语句中有distinct标志,则可以直接子查询展开;
- 如果内层查询结果没有重复元组,则可以展开。
子查询展开的具体步骤如下:
- 将子查询和上层查询的from子句连接为同一个from子句,并且修改相应的运行参数;
- 将子查询的谓词符号进行相应修改(如IN修改为=ANY);
- 将子查询的where条件作为一个整体与上层查询的where条件进行合并,并用and连接,从而保证新生成的谓词与原谓词的语义相同,成为一个整体。
(3) 聚集子查询消除
这种方法将聚集子查询的计算上推,使得子查询只需计算一次,并与父查询的部分或全表做左外连接。例如:
SELECT *
FROM t1
WHERE t1.a1 > (SELECT avg(t2.a2) FROM t2);可优化为:
SELECT t1.*
FROM t1, (SELECT avg(t2.a2) FROM t2) as tm(avg_a2) )
WHERE t1.a1 ? tm.avg_a2;(4) 其他
此外还有利用窗口函数消除子查询、子查询推进等技术
- 针对不同类型子查询的优化方法
(1) IN类型子查询
IN类型有3种格式:
格式一:
outer_expr [not] in (select inner_expr from ... where subquery_where)格式二:
outer_expr = any (select inner_expr from ... where subquery_where)格式三:
(oe_1, ..., oe_N) [not] in (select ie_1, ..., ie_N from ... where subquery_where)对于in类型子查询的优化,IN类型子查询优化的几种情况
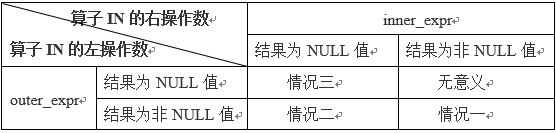
情况一:outer_expr和inner_expr均为非NULL值。
优化后的表达式为:
exists (select 1 from ... where subquery_where and outer_expr=inner_expr)子查询优化需要满足2个条件:
outer_expr和inner_expr不能为NULL;
不需要从结果为FALSE的子查询中区分NULL。
情况二:outer_expr是非空值。
优化后的表达式为:
exists (select 1 from ... where subquery_where and
(outer_expr=inner_expr or inner_expr IS NULL);情况三:outer_expr为空值。
则原表达式等价为:
NULL in (select inner_expr FROM ... where subquery_where)当outer_expr为空时,如果子查询结果为:
- NULL,select语句产生任意行数据;
- FALSE,select语句不产生数据。
对上面的等价形式,还有2点需说明:
- 谓词IN等价于=ANY。如:以下2条SQL语句是等价的。
select col1 from t1 where col1 =ANY (select col1 from t2);
select col1 from t1 where col1 IN (select col1 from t2);- 带有IN谓词的子查询,如果满足上述3种情况,可做等价变换,把外层条件下推到子查询中,变形为EXISTS类型的逻辑表达式判断。而EXISTS子查询可以被半连接算法实现优化。
(2) ALL/ANY/SOME类型子查询
ALL/ANY/SOME子查询格式如下:
outer_expr operator ALL (subquery)
outer_expr operator ANY (subquery)
outer_expr operator SOME (subquery)其中,operator是操作符,可以是>、>=、=、<、<=中任何一个。其中,
- =ANY与IN含义相同,可采用IN子查询优化方法;
- SOME与ANY含义相同;
- NOT IN 与 <>ALL含义相同;
如果子查询中没有group by子句,也没有聚集函数,则以下表达式可以使用聚集函数MAX/MIN做等价转换:
val>=ALL (select ...)等价变换为:val>= (select MAX...)val<=ALL (select ...)等价变换为:val<= (select MAX...)val>=ANY (select ...)等价变换为:val>= (select MIN...)val>=ANY (select ...)等价变换为:val>= (select MAX...)
(3) EXISTS类型子查询
存在谓词子查询格式为:[NOT] EXISTS (subquery)
需要注意几点:
- EXISTS(subquery)值为TRUE/FALSE,不关心subquery返回的内容。
- EXISTS(subquery)自身有”半连接”的语义,部分DBMS用半连接来实现它;NOT EXISTS通常会被标识为”反半连接”处理。
- IN(subquery)等子查询可以被转换为EXISTS(subquery)格式。
所谓半连接(Semi Join),是一种特殊的连接类型。如果用”t1.x semi= t2.y”来表示表T1和表T2做半连接,则其含义是:只要在表T2中找到一条记录满足t1.x=t2.y,则马上停止搜索表T2,并直接返回表T1中满足条件t1.x=t2.y的记录,因此半连接的执行效率高于普通的内连接。
4.2.2.2 等价谓词重写
等价谓词重写包括:LIKE规则、BETWEEN-AND规则、IN转换OR规则、IN转换ANY规则、OR转换ANY规则、ALL/ANY转换集函数规则、NOT规则等,相关原理比较简单,有兴趣的同学可以自行查找相关查询重写规则。
4.2.2.3 条件化简
WHERE、HAVING和ON条件由许多表达式组成,而这些表达式在某些时候彼此间存在一定的联系。利用等式和不等式性质,可将WHERE、HAVING和ON条件简化,但不同数据库的实现可能不完全相同。
将WHERE、HAVING和ON条件简化的方式通常包括如下几个:
去除表达式中冗余的括号:以减少语法分析时产生的AND和OR树的层次;
常量传递:对不同关系可使用条件分离后有效实施”选择下推”,从而减小中间关系的规模。如:
col1=col2 AND col2=3可化简为:col1=3 AND col2=3操作符=、<、>、<=、>=、<>、LIKE中的任何一个,在
col1<操作符>col2条件中都会发生常量传递消除死码。化简条件,将不必要的条件去除。如:
WHERE (0>1 AND s1=5),0>1使得AND为恒假,去除即可。表达式变换。化简条件(如反转关系操作符的操作数顺序),从而改变某些表的访问路径。如:-a=3可化简为a=-3,若a上有索引,则可利用。
不等式变换。化简条件,将不必要的重复条件去除。如:
a>10 AND b=6 AND a>2可化简为:a>10 AND b=6。布尔表达式变换。包括:
- 谓词传递闭包。如:
a>b AND b>2可推导出a>2,减少a、b比较元组数。 - 任何一个布尔表达式都能被转换为一个等价的合取范式。一个合取项为假,则整个表达式为假。
4.3 物理优化
代数优化改变查询语句中操作的次序和组合,但不涉及底层的存取路径。物理优化就是要选择高效合理的操作算法或存取路径,求得优化的查询计划,达到查询优化的目标。
查询优化器在物理优化阶段,主要解决的问题是:
- 从可选的单表扫描方式中,挑选什么样的单表扫描方式最优?
- 对于两表连接,如何连接最优?
- 对于多表连接,哪种连接顺序最优?
- 对于多表连接,是否需要对每种连接顺序都探索?如果不全部探索,如何找到一种最优组合?
选择的方法可以是:
- 基于规则的启发式优化。
- 基于代价估算的优化。
- 两者结合的优化方法。常常先使用启发式规则选取若干个较优的候选方案,减少代价估算的工作量,然后分别计算这些候选方案的执行代价,较快地选出最终的优化方法。
启发式规则优化是定性的选择,比较粗糙,但是实现简单而且优化本身的代价较小,适合解释执行的系统。因为解释执行的系统,其优开销包含在查询总开销之中,在编译执行的系统中,一次编译优化,多次执行,查询优化和查询执行是分开的,因此,可以用精细复杂一些的基于代价的优化方法。
4.3.1 基于代价的优化
4.3.1.1 查询代价估算
查询代价估算基于CPU代价和I/O代价,计算公式如下:
总代价 = I/O代价 + CPU代价
COST = P * a_page_cpu_time + W * T其中:
P是计划运行时访问的页面数,a_page_cpu_time是每个页面读取的时间开销,其乘积反映了I/O开销。
T为访问的元组数,如果是索引扫描,还要考虑索引读取的开销,反映了数据读取到内存的CPU开销。
W为权重因子,表明I/O到CPU的相关性,又称选择率(selectivity),用于表示在关系R中,满足条件“A a”的元组数与R的所有元组数N的比值。
选择率在代价估算模型中占有重要地位,其精确程度直接影响最优计划的选取。选择率计算常用方法如下:
- 无参数方法:使用ad hoc(点对点)数据结构或直方图维护属性值的分布,直方图最常用;
- 参数法:使用具有一些自由统计参数(参数是预先估计出来的)的数学分布函数逼近真实分布;
- 曲线拟合法:为克服参数法的不灵活性,用一般多项式来标准最小方差来逼近属性值的分布;
- 抽样法:从数据库中抽取部分样本元组,针对这些样本进行查询,然后收集统计数据;
- 综合法:将以上几种方法结合起来,如抽样法和直方图法结合。
由于其中I/O代价占比最大,通常以I/O代价为主来进行代价估算。
- 全表扫描算法的代价估算公式
如果基本表大小为 B 块,全表扫描算法的代价 cost = B;
如果选择条件是”码=值”,则平均搜索代价 cost = B/2。
- 索引扫描算法的代价估算公式
如果选择条件为”码=值”,则采用该表的主索引,若为B+树,设索引层数为L,需要存取B+树中从根节点到叶节点L块,再加上基本表中该元组所在的那一块,cost=L+1。
如果选择条件涉及非码属性,若为B+树索引,选择条件是相等比较,S为索引选择基数(有S个元组满足条件),假设满足条件的元组保存在不同块上,则最坏情况下cost=L+S。
l 若比较条件为>,>=,<,<=,假设有一半元组满足条件,则需要存取一半的叶节点,并通过索引访问一半的表存储块,cost=L+Y/2+B/2。若可以获得更准确的选择基数,可进一步修正Y/2与B/2。
3.嵌套循环连接算法的代价估算公式
嵌套循环连接算法的代价为:cost=Br+BrBs/(K-1), 且K<B(R)<B(S),其中K表示缓冲区大小为K块;
若需要把中间结果写回磁盘,则代价为:cost=Br+BrBs/(K-1) + (Frs*Nr*Ns)/Mrs。Frs为连接选择率,表示连接结果数的比例,Mrs为块因子,表示每块中可以存放的结果元组数目。
4.排序合并连接算法的代价估算公式
如 果 连 接 表 已 经 按 照 连 接 属 性 排 好 序 , 则 cost =Br+Bs+(Frs*Nr*Ns)/Mrs。
如果必须对文件排序,需要在代价函数中加上排序的代价对 于 包 含 B 个 块 的 文 件 排 序 的 代 价 大 约 是:cost =(2*B)+(2*B*log2B)。
4.3.1.2 基于代价的连接顺序选择
多表连接算法实现的是在查询路径生成的过程中,根据代价估算,从各种可能的候选路径中找出最优的路径。它需要解决两个问题:
- 多表连接的顺序
- 多表连接的搜索空间:N个表的连接可能有N!种连接组合,这可能构成一个巨大的搜索空间。如何将搜索空间限制在一个可接受的范围内,并高效生成查询执行计划将成为一个难点。
多表间的连接顺序表示了查询计划树的基本形态。在1990年,Schneder等人在研究查询树模型时提出了左深树,右深树和紧密树3种形态
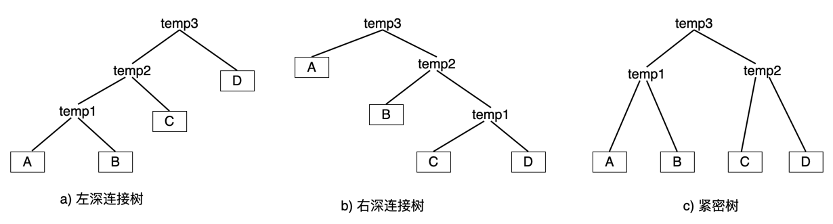
即使是同一种树的生成方式,也有细节需要考虑。如图5-1-a中{A,B}和{B,A}两种连接方式开销可能不同。比如最终连接结果{A,B,C}则需要验证比较6种连接方式,找出最优的一种作为下次和其他表连接的依据。
多表连接搜索最优查询树,有很多算法,如启发式、分枝界定计划枚举、贪心、动态规划、爬山法、System R优化方法等。其中,常用算法如下。
动态规划
在数据库领域,动态规划算法主要解决多表连接的问题。它是自底向上进行的,即从叶子开始做第一层,然后开始对每层的关系做两两连接(如果满足内连接进行两两连接,不满足则不可对全部表进行两两连接),构造出上层,逐次递推到树根。以下介绍具体步骤:
初始状态:构造第一层关系,即叶子结点,每个叶子对应一个单表,为每一个待连接的关系计算最优路径(单表的最优路径就是单表的最佳访问方式,通过评估不同的单表的数据扫描方式代价,找出代价最小的作为每个单表的局部最优路径)
归纳:当第1层到第n-1层的关系已经生成,那么求解第n层的关系方法为:将第n-1层的关系与第一层中的每个关系连接,生成新的关系(对新关系的大小进行估算),放于第n层,且每一个新关系,均求解最优路径。每层路径的生成都是基于下层生成的最优路径,这满足最优化原理的要求。
还有的改进算法,在生成第n层的时候,除了通过第n-1层和第一层连接外,还可以通过第n-2层和第二层连接…。
PostgreSQL查询优化器求解多表连接时,采用了这种算法。
启发式算法
启发式算法是相对最优化算法提出的,是一个基于直观或者经验构造的算法,不能保证找到最好的查询计划。在数据库的查询优化器中,启发式一直贯穿于整个查询优化阶段,在逻辑查询优化阶段和物理查询优化阶段,都有一些启发式规则可用。PostgreSQL,MySQL,Oracle等数据库在实现查询优化器时,采用了启发式和其他方式相结合的方式。
物理查询优化阶段常用启发式规则如下:
- 关系R在列X上建立索引,且对R的选择操作发生在列X上,则采用索引扫描方式;
- R连接S,其中一个关系上的连接列存在索引,则采用索引连接且此关系作为内表;
- R连接S,其中一个关系上的连接列是排序的,则采用排序连接比hash连接好。
贪心算法
贪心算法最后得到的是局部最优解,不一定全局最优,其实现步骤如下:
(1) 初始,算法选出的候选对象集合为空;
(2) 根据选择函数,从剩余候选对象中选出最有可能构成解的对象;
(3) 如果集合中加上该对象后不可行,那么该对象就被丢弃并不再考虑;
(4) 如果集合中加上该对象后可行,就加到集合里;
(5) 扩充集合,检查该集合是否构成解;
(6) 如果贪心算法正确工作,那么找到的第一个解通常都是最优的,可以终止算法;
(7) 继续执行第二步。
MySQL查询优化器求解多表连接时采用了这种算法。
System-R算法
对自底向上的动态规划算法进行了改进,主要思想是把子树的查询计划的最优查询计划和次优查询计划保留,用于上层的查询计划生成,以便使得查询计划总体上最优。
多表连接常用算法比较
| 算法名称 | 特点与适用范围 | 缺点 |
|---|---|---|
| 启发式算法 | 适用于任何范围,与其它算法结合,能有效提高整体效率 | 不知道得到的解是否最优 |
| 贪婪算法 | 非穷举类型的算法。适合解决较多关系的搜索 | 得到局部最优解 |
| 爬山法 | 适合查询中包含较多关系的搜索,基于贪婪算法 | 随机性强,得到局部最优解 |
| 遗传算法 | 非穷举类型的算法。适合解决较多关系的搜索 | 得到局部最优解 |
| 动态规划算法 | 穷举类型的算法。适合查询中包含较少关系的搜索,可得到全局最优解 | 搜索空间随关系个数增长呈指数增长 |
| System R优化 | 基于自底向上的动态规划算法,为上层提供更多可能的备选路径,可得到全局最优解 | 搜索空间可能比动态规划算法更大一些 |
4.3.2 基于规则的优化
基于代价优化的一个缺点是优化本身的代价。因此,查询优化器使用启发式方法来减少优化代价。
- 选择操作的启发式规则:
1) 对于小关系,全表扫描;
2) 对于大关系:
(1) 若选择条件是主码,则可以选择主码索引,因为主码索引一般是被自动建立的;
(2) 若选择条件是非主属性的等职查询,并且选择列上有索引,如果选择比例较小(10%)可以使用索引扫描,否则全表扫描;
(3) 若选择条件是属性上的非等值查询或者范围查询,同上;
(4) 对于用and连接的合取选择条件,若有组合索引,优先用组合索引方法;如果某些属性上有一般索引,则用索引扫描,否则全表扫描;
(5) 对于用OR连接的析取选择条件,全表扫描。- 连接操作的启发式规则
1) 若两个表都已经按连接属性排序,则选用排序-合并算法;
2) 若一个表在连接属性上有索引,则使用索引连接方法;
3) 若其中一个表较小,则选用hash join;
4) 最后可以使用嵌套循环,小表作为外表。
第五章 事务处理
5.1 事务概念
在数据库系统中,事务是指由一系列数据库操作组成的一个完整的逻辑过程。数据库提供了增、删、改、查等几种基础操作,用户可以灵活地组合这几种操作来实现复杂的语义。在很多场景下,用户希望一组操作可以做为一个整体一起生效,这就是事务的产生背景。
例如,一个银行转帐业务,在数据库中需要通过两个修改操作来实现:
- 从账户A扣除指定金额;
- 向账户B添加指定金额。
这两个操作构成了一个完整的逻辑过程,不可拆分。如果第一个操作成功而第二个操作失败,说明转账没有成功。在这种情况下,对于银行来说,数据库中的账户数据是处于一种不正确的状态的,必须撤销掉第一个操作对数据库的修改,让账户数据恢复到转账前的状态。由此例可见,事务是数据库状态变更的基本单元,在事务将数据库从一个正确状态变更到另一个正确状态的过程中,数据库的那些中间状态,既不应该被其他事务看到或干扰,也不应该在事务结束后依然保留。
根据以上描述的事务概念,事务应具有四个特性,称为事务的ACID特性。它们分别是:
- 原子性 (Atomicity):一个事务中的所有操作,要么全做,要么全不做。事务如果在执行过程中发生错误,该事务修改过的数据应该被恢复到事务开始前的状态,就像这个事务从来没有执行过一样。
- 一致性 (Consistency):当数据库只包含成功事务提交的结果时,称数据库处于一致性状态。事务执行的结果必须使数据库从一个一致性状态变到另一个一致性状态。由此可见,一致性与原子性是密切相关的。
- 隔离性 (Isolation):一个事务的执行不能被其他事务干扰。DBMS允许多个并发事务同时执行,隔离性可以防止多个事务并发执行时由于相互干扰而导致数据的不一致。
- 持久性 (Durability):事务处理结束后,对数据的修改就是永久的,即便系统故障也不会丢失。
在数据库运行过程中,刚插入的数据往往不会直接写入磁盘,而是先缓存在内存中。对于一个运行中的数据库,可以将其地址空间简单分成三个部分:
- 1.持久化保存数据的磁盘空间
- 2.缓冲区对应的内存或虚拟内存空间
- 3.事务的局部地址空间〈也在内存中)
事务要读取数据,首先要将数据取到缓冲区中,然后缓冲区的数据可以被事务读取到局部空间。事务的写入过程与此相反,先在局部空间中创建新值,然后再将新数据拷贝到缓冲区中。缓冲区中的数据通常是由缓冲区管理器决定何时写入磁盘,而不是立刻持久化到磁盘。
在SQL中,开始和结束事务的语句如下:
- BEGIN TRANSACTION:开始一个事务。除了用该语句显式地开始一个事务,DBMS也允许隐式的开始一个事务。隐式开始事务时无需执行任何语句,每当用户连接成功,即开始一个事务,前一个事务结束时,即自动开始下一个事务。
- COMMIT:提交一个事务。此语句表示事务正常结束,DBMS应永久保存该事务对数据库的修改。
- ROLLBACK:回滚一个事务。此语句表示事务异常结束,DBMS应撤销该事务对数据库的所有修改。需要注意的是,当事务发生故障时,即使用户没有显式执行ROLLBACK语句,DBMS也应自动回滚事务。
一个支持事务的DBMS必须能保证事务的ACID特性,这部分工作是由事务处理机制来负责的。事务处理机制又分为并发控制机制和故障恢复机制两部分,以下分别介绍。
5.2 并发控制
所谓并发操作,是指在多用户共享的数据库中,多个事务可能同时对同一数据进行操作。如果对这些操作不加控制,则可能导致数据的不一致问题。因此,为了保证事务的一致性和隔离性,DBMS需要对并发操作进行正确调度。这就是并发控制机制的任务。
5.2.1 并发错误
并发操作带来的数据不一致性包括丢失修改、读脏和不可重复读。
丢失修改
两个以上事务从数据库中读入同一数据并修改,其中一个事务(后提交的事务)的提交结果破坏了另一事务(先提交的事务)的提交结果,导致先提交的事务对数据库的修改被丢失。
读脏
事务读取了被其他事务修改且未提交的数据,即从数据库中读到了临时性数据。
不可重复读
一个事务读取数据后,该数据又被另一事务修改,导致前一事务无法再现前一次的读取结果。
不可重复读又可分为两种情况:一种情况是第一次读到的数据的值在第二次读取时发生了变化;还有一种情况是事务第二次按相同条件读取数据时,返回结果中多了或者少了一些记录。后者又被称为幻读。
5.2.2 并发控制的正确性标准
并发控制机制的任务就是对并发事务进行正确的调度,但是什么样的调度才是正确的呢?我们需要一个正确性的判断标准。
5.2.2.1 可串行化
串行调度是指多个事务依序串行执行,仅当一个事务的所有操作执行完后才执行另一个事务。这种调度方式下,不可能出现多个事务同时访问同一数据的问题,自然也就不可能出现并发错误。串行调度显然是正确的,但是串行调度无法充分利用系统资源,因此其效率显然也是用户难以接受的。
并发调度是指在数据库系统中同时执行多个事务。DBMS对多个并发事务进行调度时,可能产生多个不同的调度序列,从而得到不同的执行结果。如何判断某个调度是不是正确呢?如果这些并发事务的执行结果与它们按某一次序串行执行的结果相同,则认为该并发调度是正确的,我们称之为可串行化调度。
5.2.2.2 冲突可串行化
可串行化是并发控制的正确性准则。但是按照可串行化的定义,如果想要判断一个并发调度是不是可串行化调度,需要知道这批事务所有可能的串行调度的结果,然后将该并发调度的结果与这些结果进行比较,这显然是难以实施的。因此,我们需要一种可操作的判断标准,即冲突可串行化。
冲突可串行化是可串行化的充分条件。如果一个并发调度是冲突可串行化的,那么它一定是可串行化的。在定义冲突可串行化之前,需要先了解什么是冲突操作。
冲突操作是指不同的事务对同一个数据的读写操作或写写操作。例如,事务1对数据A的读操作”r1(A)”与事务2对数据A的写操作”w2(A)”就是一对冲突操作。
我们规定,不同事务的冲突操作和同一事务的两个操作是不能交换的。因为如果改变冲突操作的次序,则最后的数据库状态会发生变化。按照这个规定,在保证一个并发调度中的冲突操作次序不变的情况下,如果通过交换两个事务的非冲突操作,能够得到一个串行调度,则称该并发调度是冲突可串行化的。
例如,对于以下两个并发调度序列:
SC1:r1(A) w1(B) r2(B) w1(C) w2(B)
SC2:r1(B) r2(A) w1(A) w2(B)
SC1就是冲突可串行化的,因为可以通过交换非冲突操作3和4得到一个串行调度序列。而SC2则是非冲突可串行化的,因为操作2和3是冲突操作,无法交换。
5.2.3 事务隔离级别
可串行化是一个很严格的正确性标准。在实际应用中,有时候可能会希望降低这个标准,通过牺牲一定的正确性,达到提高并发度的目的。为此,SQL标准将事务的隔离程度划分为四个等级,允许用户根据需要自己指定事务的隔离级。这四种隔离级包括读未提交(Read Uncommitted)、读提交(Read Committed)、可重复读(Repeatable Read)和可串行化(Serializable)。
- 读未提交:在该隔离级别,事务可以看到其他未提交事务的执行结果,即允许读脏数据。
- 读提交:这是大多数DBMS的默认隔离级别,它要求事务只能看见已提交事务所做的修改,因此可以避免读脏数据。但是由于在某个事务的执行期间,同一个数据可能被另一个事务修改并提交,所以该事务对该数据的两次读取可能会返回不同的值,即出现不可重复读错误。
- 可重复读:在该隔离级别,同一事务多次读取同一数据时,总是会读到同样的值。不过理论上,该隔离级不能避免幻读,即使用相同条件多次读取时,满足读取条件的数据的数量可能有变化,比如多出一些满足条件的数据。
- 可串行化:这是最高的隔离级别,能够避免所有并发错误。可串行化的概念前面已经介绍过,此处不再赘述。
5.3 封锁机制
5.3.1什么是封锁
封锁机制是一种常用的并发控制手段,它包括三个环节:第一个环节是申请加锁,即事务在操作前对它要使用的数据提出加锁请求;第二个环节是获得锁,即当条件满足时,系统允许事务对数据加锁,使事务获得数据的控制权;第三个环节是释放锁,即完成操作后事务放弃数据的控制权。为了达到并发控制的目的,在使用时事务应选择合适的锁,并遵从一定的封锁协议。
基本的封锁类型有两种:排它锁(Exclusive Locks,简称X锁)和共享锁(Share Locks,简称S锁)。
排它锁
排它锁也称为独占锁或写锁。一旦事务T对数据对象A加上了排它锁(X锁),则其他任何事务不能再对A加任何类型的锁,直到T释放A上的锁为止。
共享锁
共享锁又称读锁。如果事务T对数据对象A加上了共享锁(S锁),其他事务对A就只能加S锁而不能加X锁,直到事务T释放A上的S锁为止。
5.3.2 封锁协议
简单地对数据加X锁和S锁并不能保证数据库的一致性。在对数据对象加锁时,还需要约定一些规则,包括何时申请锁、申请什么类型的锁、何时释放锁等,这些规则称为封锁协议。不同的规则形成了各种不同的封锁协议。封锁协议分三级,它们对并发操作带来的丢失修改、读脏和不可重复读等并发错误,可以在不同程度上予以解决。
一级封锁协议
一级封锁协议是指事务T在修改数据之前必须先对其加X锁,直到事务结束才释放。
一级封锁协议可有效地防止丢失修改,并能够保证事务T的可恢复性。但是,由于一级封锁没有要求对读数据进行加锁,所以不能防止读脏和不可重复读。遵循一级封锁协议的事务可以达到读未提交的事务隔离级。
二级封锁协议
二级封锁协议是指事务T在修改数据之前必须先加X锁,直到事务结束才释放X锁;在读取数据之前必须先加S锁,读完后即可释放S锁。
二级封锁协议不但能够防止丢失修改,还可进一步防止读脏。遵循二级封锁协议的事务可以达到读提交的事务隔离级。
三级封锁协议
三级封锁协议是事务T在读取数据之前必须先对其加S锁,在修改数据之前必须先对其加X锁,直到事务结束后才释放所有锁。
由于三级封锁协议强调即使事务读完数据A之后也不释放S锁,从而使得别的事务无法更改数据A,所以三级封锁协议不但能够防止丢失修改和读脏,而且能够防止不可重复读。遵循三级封锁协议的事务至少可以达到可重复读的事务隔离级,至于是否能到达可串行化级别,则取决于S锁的粒度。比如,如果只对要读取的记录加锁,则无法避免幻读问题;但如果是对整个表加锁,则幻读问题可以避免,代价是并发度的下降。
5.3.3 封锁的实现
锁管理器可以实现为一个进程或线程,它从事务接受请求消息并反馈结果消息。对于事务的加锁请求消息,锁管理器返回授予锁消息,或者要求事务回滚的消息(发生死锁时);对于事务的解锁请求消息,只需返回一个确认消息,但可能触发锁管理器向正在等待该事务解锁的其他事务发送授予锁消息。
锁管理器使用以下数据结构:
- 为目前已加锁的每个数据对象维护一个链表,链表中的每个结点代表一个加锁请求,按请求到达的顺序排序。一个加锁请求包含的信息有:提出请求的事务ID,请求的锁的类型,以及该请求是否已被授予锁。
- 使用一个以数据对象ID为索引的散列表来查找数据对象(如果有的话),这个散列表叫做锁表。
下图是一个锁表的示例图,该表包含5个不同的数据对象14、17、123、144和1912的锁。锁表采用溢出链表示法,因此对于锁表的每一个表项都有一个数据对象的链表。每一个数据对象都有一个已授予锁或等待授予锁的事务请求列表,已授予锁的请求用深色阴影方块表示,等待授予锁的请求则用浅色阴影方块表示。 例如,事务T23在数据对象17和1912上已被授予锁,并且正在等待对数据对象14加锁。
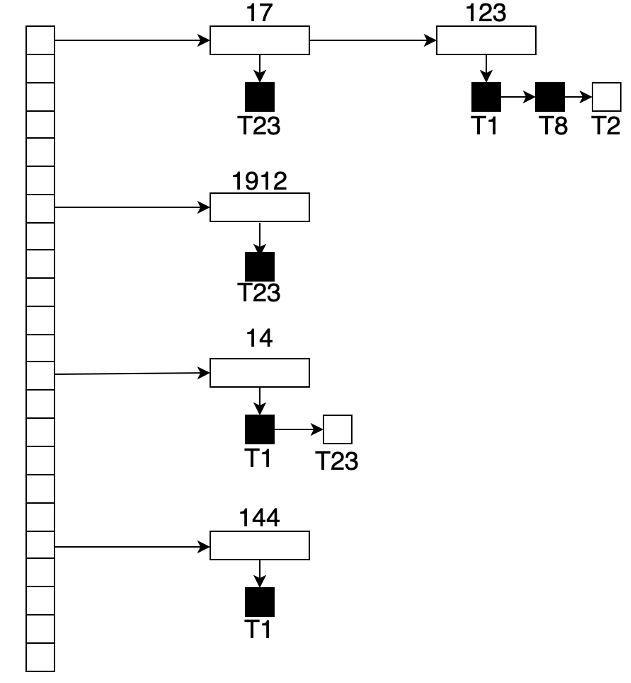
虽然图没有标示出来,但对锁表还应当维护一个基于事务标识符的索引,这样它可以快速确定一个给定事务持有的锁的集合。
锁管理器这样处理请求:
- 当一条加锁请求消息到达时,如果锁表中存在相应数据对象的链表,则在该链表末尾增加一个请求;否则,新建一个仅包含该请求的链表。对于当前没有加锁的数据对象,总是满足事务对其的第一次加锁请求,但当事务向已被加锁的数据对象申请加锁时,只有当该请求与当前持有的锁相容、并且所有之前的请求都已授予锁的条件下,锁管理器才为该请求授予锁,否则,该请求只能等待。
- 当锁管理器收到一个事务的解锁消息时,它先找到对应的数据对象链表,删除其中该事务的请求,然后检查其后的请求,如果有,则看该请求能否被满足,如果能,锁管理器授权该请求,再按相同的方式处理后续的请求。
- 如果一个事务被中止,锁管理器首先删除该事务产生的正在等待加锁的所有请求;当系统采取适当动作撤销了该事务后,该中止事务持有的所有锁也将被释放。
这个算法保证了锁请求无饿死现象,因为在先接收到的请求正在等待加锁时,后来的请求不可能获得授权。
为了避免消息传递的开销,在许多DBMS中,事务通过直接更新锁表来实现封锁,而不是向锁管理器发送请求消息。事务加锁和解锁的操作逻辑与上述锁管理器的处理方法类似,但是有两个明显的区别:
- 由于多个事务可以同时访问锁表,因此必须确保对锁表的互斥访问。
- 如果因为锁冲突而不能立刻获得锁,加锁事务需要知道自己何时可以被授予锁,解锁事务需要标记出那些可以被授予锁的事务并通知它们。这个功能可以通过操作系统的信号量机制来实现。
5.3.4 死锁处理
封锁机制有可能导致死锁,DBMS必须妥善地解决死锁问题,才能保障系统的正常运行。
如果事务T1和T2都需要修改数据Rl和R2,并发执行时Tl封锁了数据R1,T2封锁了数据R2;然后T1又请求封锁R2,T2又请求封锁Rl;因T2已封锁了R2,故T1等待T2释放R2上的锁。同理,因T1已封锁了R1,故T2等待T1释放R1上的锁。由于Tl和T2都没有获得全部需要的数据,所以它们不会结束,只能继续等待。这种多事务交错等待的僵持局面称为死锁。
一般来讲,死锁是不可避免的。DBMS的并发控制子系统一旦检测到系统中存在死锁,就要设法解除。通常采用的方法是选择一个处理死锁代价最小的事务,将其中止,释放此事务持有的所有的锁,使其他事务得以继续运行下去。当然,被中止的事务已经执行的所有数据修改操作都必须被撤销。
数据库中解决死锁问题主要有两类方法:一类方法是允许发生死锁,然后采用一定手段定期诊断系统中有无死锁,若有则解除之,称为死锁检测;另一类方法是采用一定措施来预防死锁的发生,称为死锁预防。
5.3.4.1 死锁检测
锁管理器通过waits-for图记录事务的等待关系,如图6-2所示。其中结点代表事务,有向边代表事务在等待另一个事务解锁。当waits-for图出现环路时,就说明出现了死锁。锁管理器会定时检测waits-for图,如果发现环路,则需要选择一个合适的事务中止它。
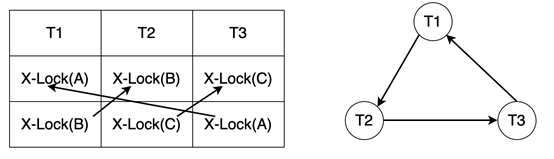
图6-2 waits-for图示例图
5.3.4.2 死锁避免
当事务请求的锁与其他事务出现锁冲突时,系统为防止死锁,杀死其中一个事务。选择要杀死的事务时,一般持续越久的事务,保留的优先级越高。这种防患于未然的方法不需要waits-for图,但提高了事务被杀死的比率。
5.3.5 封锁粒度
封锁粒度是指封锁对象的大小。封锁对象可以是逻辑单元,也可以是物理单元。以关系数据库为例,封锁对象可以是属性值、属性值的集合、记录、表、直至整个数据库;也可以是一些物理单元,例如页(数据页或索引页)、块等。封锁粒度与系统的并发度及并发控制的开销密切相关。封锁的粒度越小,并发度越高,系统开销也越大;封锁的粒度越大,并发度越低,系统开销也越小。
如果一个DBMS能够同时支持多种封锁粒度供不同的事务选择,这种封锁方法称为多粒度封锁。选择封锁粒度时应该综合考虑封锁开销和并发度两个因素,选择适当的封锁粒度以求得最优的效果。通常,需要处理一个表中大量记录的事务可以以表为封锁粒度;需要处理多个表中大量记录的事务可以以数据库为封锁粒度;而对于只处理少量记录的事务,则以记录为封锁粒度比较合适。
5.4 故障恢复
故障恢复机制是在数据库发生故障时确保数据库一致性、事务原子性和持久性的技术。当崩溃发生时,内存中未提交到磁盘的所有数据都有丢失的风险。故障恢复的作用是防止崩溃后的信息丢失。
故障恢复机制包含两个部分:
- 为了确保DBMS能从故障中恢复,在正常事务处理过程中需要执行的操作,如登记日志、备份数据等。
- 发生故障后,将数据库恢复到原子性、一致性和持久性状态的操作。
5.4.1 故障分类
由于DBMS根据底层存储设备被划分为不同的组件,因此DBMS需要处理许多不同类型的故障。
事务故障
一个事务出现错误且必须中止,称其为事务故障。可能导致事务失败的两种错误是逻辑错误和内部状态错误。逻辑错误是指事务由于某些内部条件无法继续正常执行,如非法输入、找不到数据、溢出等;内部状态错误是指系统进入一种不良状态,使当前事务无法继续正常执行,如死锁。
系统故障
系统故障是指导致系统停止运转、需要重新启动的事件。系统故障可能由软件或硬件的问题引起。软件问题是指由于DBMS的实现问题(如未捕获的除零异常)导致系统不得不停止;硬件问题是指DBMS所在的计算机出现崩溃,如系统突然掉电、CPU故障等。发生系统故障时,内存中的数据会丢失,但外存数据不受影响。
介质故障
介质故障是指当物理存储损坏时发生的不可修复的故障,如磁盘损坏、磁头碰撞、强磁场干扰等。当存储介质失效时,DBMS必须通过备份版本进行恢复。
5.4.2 缓冲池管理策略
缓冲池管理策略是指,对于已提交和未提交的事务,它们在内存缓冲池中修改的数据页被写出到磁盘的时机。
对于已提交事务,存在两种策略:
- FORCE:事务提交时必须强制将其修改的数据页写盘;
- NOFORCE:允许在事务提交后延迟执行写盘操作。
对于未提交事务,也存在两种策略:
- STEAL:允许在事务提交前就将其修改的数据页写盘;
- NOSTEAL:不允许在事务提交前执行写盘操作。
对于恢复来说,FORCE+ NOSTEAL是最简单的策略,但是这种策略的一个缺点是要求内存能放下事务需要修改的所有数据,否则该事务将无法执行,因为DBMS不允许在事务提交之前将脏页写入磁盘。
从高效利用内存和降低磁盘I/O开销的角度出发,NOFORCE+ STEAL策略是最灵活的,这也是很多DBMS采用的策略。在这种策略下,一旦发生故障,恢复机制可能需要执行以下操作:
- UNDO:发生故障时,尚未完成的事务的结果可能已写入磁盘,为保证数据一致性,需要清除这些事务对数据库的修改。
- REDO:发生故障时,已完成事务提交的结果可能尚未写回到磁盘,故障使得这些事务对数据库的修改丢失,这也会使数据库处于不一致状态,因此应将这些事务已提交的结果重新写入磁盘。
为了保证在恢复时能够得到足够的信息进行UNDO和REDO,DBMS在事务正常执行期间需要登记事务对数据库所做的修改,这就是日志机制。
5.4.3 日志
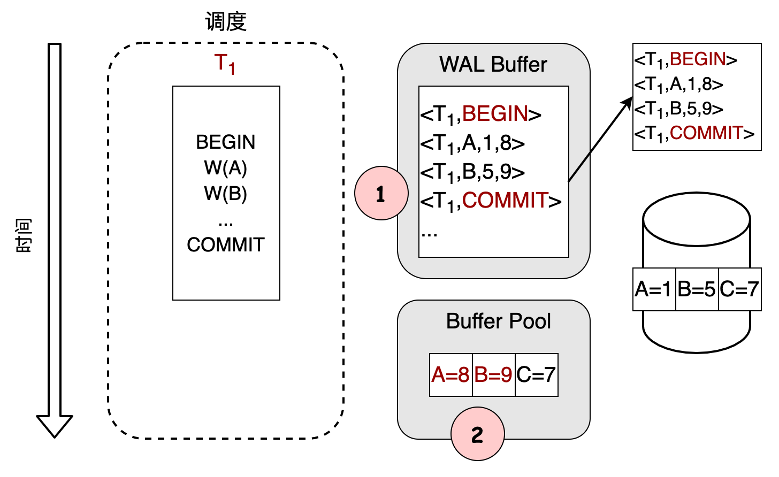
5.4.3.1 日志的原理
日志是由日志记录构成的文件,几乎所有DBMS都采用基于日志的恢复机制。它的基本思路是:DBMS在对磁盘页面进行修改之前,先将其对数据库所做的所有更改记录到磁盘上的日志文件中,日志文件包含足够的信息来执行必要的UNDO和REDO操作,以便在故障后恢复数据库。DBMS必须先将对数据库对象所做修改的日志记录写入日志文件,然后才能将该对象刷新到磁盘,这一过程称为WAL(Write Ahead Log)。WAL的执行过程如图6-3所示。事务开始后,所有对数据库的修改在发送到缓冲池之前都被记录在内存中的WAL缓冲区中。事务提交时,必须把WAL缓冲区刷新到磁盘。一旦WAL缓冲区被安全地写进磁盘,事务的修改结果就也可以写盘了。
日志文件中应该记录以下信息:
- l 事务开始时,向日志中写入一条该事务的开始记录。
- l 事务结束时,向日志中写入一条该事务的结束记录,结束记录包括两类:正常结束记录,和异常结束记录。
- 事务对每个数据对象的修改操作对应一条日志记录,其中包含以下信息:
- 事务ID
- 对象ID
- 修改前的值(用于UNDO)
- 修改后的值(用于REDO)
将日志记录从日志缓冲区写入磁盘的时机有这样几个:
- 接收到提交事务的命令后,在返回提交成功的消息之前,DBMS必须将该事务的所有日志记录写入磁盘。系统可以使用”组提交”的方式来批处理多个事务的提交,以降低I/O开销。
- 日志缓冲区空间不足的时候,需要将缓冲区中的日子记录写入磁盘。
- 在将一个脏数据页写入磁盘之前,与更新该页有关的所有日志记录都必须先被写入磁盘。
需要注意的是,登记日志时必须严格按事务的操作顺序记录,并且写到磁盘中的日志记录顺序必须与写入日志缓冲区的顺序完全一致。
5.4.3.2 日志的类型
根据实现时采用的恢复方法的不同,日志中记录的内容也不一样,分为以下几类。
- 物理日志:物理日志中记录的是事务对数据库中特定位置的字节级更改。例如,日志中记录的是事务对指定数据页中从指定位置开始的若干字节的修改。
- 逻辑日志:逻辑日志中记录的是事务执行的逻辑操作。例如,日志中记录的是事务执行的UPDATE、DELETE和INSERT语句。与物理日志相比,逻辑日志需要写的数据更少,因为每条日志记录可以在多个页面上更新多个元组。然而,当系统中存在并发事务时,通过逻辑日志实现恢复很困难。
- 混合日志:日志中记录的是事务对指定页面中指定槽号内元组的更改,而不是对页中指定偏移位置的更改。
5.4.4 恢复算法
5.4.4.1 事务故障的恢复
事务故障是指事务在运行至正常终止点前被终止,这时恢复子系统应利用日志文件UNDO此事务己对数据库进行的修改。事务故障的恢复应由DBMS自动完成,对用户完全透明。恢复步骤如下:
- 反向扫描日志文件,查找该事务的更新日志记录。
- 对该事务的更新操作执行逆操作, 即将日志记录中 “更新前的值” 写入数据库。如果记录中是插入操作,则逆操作相当于做删除操作:若记录中是删除操作,则逆操作相当于做插入操作;若是修改操作,则逆操作相当于用修改前的值代替修改后的值。
- 继续反向扫描日志文件,查找该事务的其他更新日志记录并做相同处理,直至读到此事务的开始标记。
5.4.4.2 系统故障的恢复
系统故障导致数据库处于不一致状态的原因,一方面是未提交事务对数据库的更新已经被写入数据库,另一方面则是已提交事务对数据库的更新没有被完全写入数据库。因此对于系统故障的恢复操作,就是要UNDO故障发生时未提交的事务,REDO已提交的事务。系统故障也是由DBMS在重启时自动完成,对用户完全透明。恢复步骤如下:
- 正向扫描日志文件,通过事务开始记录和COMMIT记录找出在故障发生前已提交的事务集合和未提交的事务集合。已提交的事务既有开始记录也有COMMIT记录,未提交的事务则只有开始记录,没有相应的COMMIT记录。将已提交的事务加入重做队列(REDO-LIST),未提交的事务加入撤销队列(UNDO-LIST)。
- 反向扫描日志文件,对UNDO-LIST中的各个事务进行UNDO处理。
- 正向扫描日志文件,对REDO-LIST中的各个事务进行REDO处理。
5.4.4.3 介质故障的恢复
发生介质故障后,磁盘上的物理数据和日志文件被破坏,这是最严重的一种故障,恢复方法是重装数据库,然后重做已完成的事务。介质故障的恢复需要用户人工介入,由DBA装入最新的数据库备份及日志文件备份,然后执行系统提供的恢复命令。
DBA装入相关备份文件后,系统执行的恢复过程与系统故障的恢复过程类似,也是通过扫描日志文件构造REDO-LIST和UNDO-LIST,然后对REDO-LIST和UNDO-LIST中的事务分别进行REDO和UNDO处理,这样就可以将数据库恢复到最近一次备份时的一致性状态。
5.4.5 检查点
以上讨论的基于日志的恢复算法存在两个问题:1. 构造REDO-LIST和UNDO-LIST需要搜索整个日志文件,耗费大量的时间;2.处理REDO-LIST时,很多事务的修改实际上已经写入了磁盘,但是仍然不得不进行REDO处理,浪费大量时间。为了解决上述问题,提高恢复效率,很多DBMS都采用了检查点技术,通过周期性地对日志做检查点来避免故障恢复时检查整个日志。
检查点技术的基本思路是:在日志文件中增加一类记录——检查点记录,并增加一个文件——重新开始文件。恢复子系统周期性地执行以下操作:
- 将日志缓冲区中的日志记录全部写入磁盘中的日志文件;
- 在日志文件中写入一个检查点记录;
- 将数据缓冲区中的数据写入磁盘;
- 将检查点记录在日志文件中的地址写入重新开始文件。
其中,检查点记录中包含以下信息:
- 检查点时刻,当前所有正在执行的事务清单
- 清单中每个事务最近一个日志记录的地址
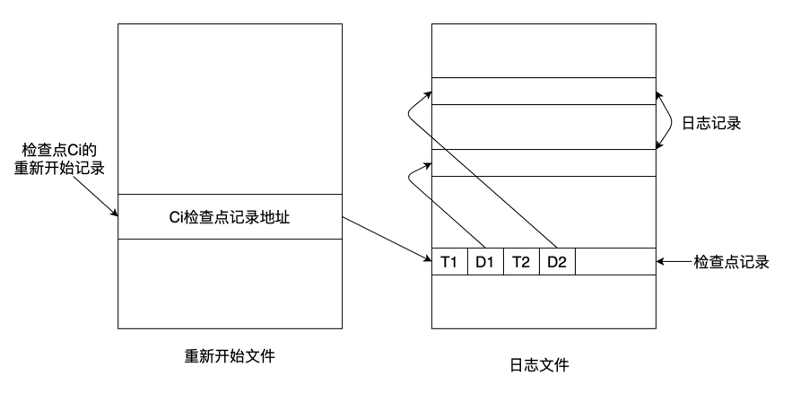
由检查点时刻系统执行的操作可知,如果一个事务在一个检查点之前已经提交了,那么它对数据库所做的修改一定都被写入了磁盘,因此在进行恢复处理时,就没有必要再对该事务执行REDO操作了。
增加了检查点之后,基于日志的恢复步骤如下:
- 从重新开始文件中找到最后一个检查点记录在日志文件中的地址,根据该地址在日志文件中找到最后一个检查点记录。
- 由该检查点记录得到检查点时刻正在执行的事务清单ACTIVE-LIST。初始化两个事务队列UNDO-LIST和REDO-LIST,令UNDO-LIST = ACTIVE-LIST,令REDO队列为空。
- 从检查点开始正向扫描日志文件直到日志文件结束,如有新开始的事务,则将其放入UNDO-LIST,如有提交的事务,则将其从UNDO-LIST队列移到REDO-LIST队列。
- 对UNDO-LIST和REDO-LIST中的每个事务,分别执行UNDO和REDO操作。
补充内容
火山模型
火山模型是数据库界已经很成熟的解释计算模型,该计算模型将关系代数中每一种操作抽象为一个 Operator,将整个 SQL 构建成一个 Operator 树,从根节点到叶子结点自上而下地递归调用 next() 函数。这里的一个造作也可以视作为一个算子。作为一个树节点,往往会存在父节点和子节点,当作为父节点时,他需要调用子节点的操作,而作为子节点则需要在被父节点调用的时候,提供数据返回给父节点。
这种设计的优点在于每一个节点(Operator),不需要关心自己的父节点和子节点是什么类型的算子和具体的实现,他只需要提供相应的接口和调用即可。树的结构是千变万化的,那么即使是有限的算子,也可以通过组成各种各样的树结构来支持复杂的查询计划。同时如果想要新增算子,也只需要实现该算子的相应接口,并加入到构建中即可,有着良好的可扩展性。
- 一般Operator的next() 接口实现分为三步
(1)调用子节点Operator的next() 接口获取一行数据(tuple)
(2)对tuple进行Operator特定的处理(如filter 或project 等)
(3)返回处理后的tuple。
所以经常能在代码中看到这样的代码:
Operator.Children.Next().例如 SQL:
SELECT Id, Name, Age, (Age - 30) * 50 AS Bonus
FROM People
WHERE Age > 30对应火山模型如下:
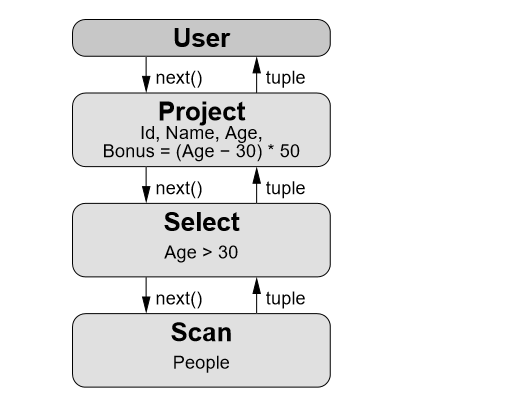
- User:客户端。负责获取用户的sql,也负责发送给客户端sql的执行结果。
- Project:垂直分割(投影),选择字段。对应于sql为:“SELECT Id, Name, Age, (Age - 30) * 50 AS Bonus”,接收子节点数据后,通过处理,得到需要返回给上层的结果值。
- Select(或 Filter):水平分割(选择),用于过滤行,也称为谓词。对应于sql为:“WHERE Age > 30”,接收子节点数据后,过滤掉不符合条件的数据。
- Scan:扫描数据。将数据从存储层拉到计算层。比如将People的表数据从磁盘拉到内存。对应sql为:“FROM People”
这里包含了 3 个 Operator,首先 User 调用最上方的 Operator(Project)希望得到 next tuple,Project 调用子节点(Select),而 Select 又调用子节点(Scan),Scan 获得表中的 tuple 返回给 Select,Select 会检查是否满足过滤条件,如果满足则返回给 Project,如果不满足则请求 Scan 获取 next tuple。Project 会对每一个 tuple 选择需要的字段或者计算新字段并返回新的 tuple 给 User。当 Scan 发现没有数据可以获取时,则返回一个结束标记告诉上游已结束。
为了更好地理解一个 Operator 中发生了什么,下面通过伪代码来理解 Select Operator:
Tuple Select::next() {
while (true) {
Tuple candidate = child->next(); // 从子节点中获取 next tuple
if (candidate == EndOfStream) // 是否得到结束标记
return EndOfStream;
if (condition->check(candidate)) // 是否满足过滤条件
return candidate; // 返回 tuple
}
}参考一个案例: select name from student where teacher = ‘Karim’
从上面的图和右边的代码可以简单的了解下火山模型的调用和实现的思路。
- Projection: 投影算子,用于获取数据中的具体需要的字段,在该案例中是Name字段。Next()中的实现会首先调用 Children的Next()方法,获取数据,并取出Name这一列返回。
- Selection:过滤算子,用于将数据中 Teacher = ‘Karim’ 的记录过滤出来,返回给上一层。Next()中的实现同样是先调用Children的Next()方法来获取数据。
- Scan:扫描算子,用于从存储节点中获取所有的数据,并返回到父节点。因为Scan一般都是叶子节点,不需要再继续要调用Children的Next()方法。
通过这种设计思路,将每个算子封装成一个Operator来独自处理,配合树结构的执行策略,有着非常优秀的可扩展性,同时兄弟节点之间的操作可以并行处理,所以火山模型同样也有着一定的并行处理能力。
在上面代码中,可以关注一个细节,也就是Next方法中其实都是只处理一行数据的,这种方式在当时是为了对内存使用的优化,那个年代的内存资源是非常昂贵的,而相比CPU的执行效率,IO执行效率会更低,所以火山模型将内存资源更多的放在IO上,而不是CPU的执行优化上。
但是现在看来,这种处理方式也会有着些许缺点,每次一整个Next调用链只会处理一行数据,效率非常的低,而同时一行数据处理就得调用多次Next()方法,大量数据处理下,函数调用的开销也会非常的大
优化方向
首先,考虑到大量虚函数的调用,那我能否写一个循环去执行 Operator 中的计算逻辑呢?执行完成后再向上传递,这样将之前的自上而下的拉模型改成了自下而上的推模型。
其次,火山模型中一次只取一条数据,如果每次取多条数据呢?因为可以将每次 next 带来的 CPU 开销被一组数据给分摊。这样当 CPU 访问元组中的某个列时会将该元组加载到 CPU Cache(如果该元组大小小于 CPU Cache 缓存行的大小), 访问后继的列将直接从 CPU Cache 中获取,从而具有较高的 CPU Cache 命中率,然而如果只访问一个列或者少数几个列时 CPU 命中率仍然不理想。即向量化/批处理模型(Vectorized / Batch Model),向量化模型 和 火山模型 类似,每个 operator 需要实现一个 next() 函数,但是每次调用 next() 函数会返回一批的元组(tuples),而不是一个元组,所以向量化模型也可称为批处理模型。 目前很多数据库采取的都是这种处理模式。
在算子间传递数据不再是一条一条记录,而是一批数据,算子每次执行的时候都会在内部攒一批数据,数据大小尽可能和CPU cache对齐,不仅大大提高了cache命中率,而且有效了减少了函数调用次数。
另外,我们再想想什么时候可以做到取多条数据同时计算呢?当然是同一列的时候,所以针对的是列存的场景,因为输入是同列的一组数据,面对的是相同的操作,这正是向量寄存器干的事情,这是 CPU 层面计算性能的优化,因此称为向量化。并且如果每次只取一列的部分数据,返回一个可以放到 CPU Cache 的向量,那么又可以利用到 CPU Cache。
火山模型中的查询并行实现
关系查询处理引擎中实现并行查询主要包括以下两个方向:
- 算子间并行(inter-operator parallelism):查询处理使用 operator 树执行,这些 operator 可以划分为多条 pipeline 在独立的进程或处理器上运行,称为算子间的并行。
- 算子内并行(intra-operator parallelism):每个 operator 的 input 数据可以被划分为不相交的子集,从而同时执行相同的 operator,称为算子内部的并行。
火山模型中负责实现并行执行的是 Exchange 运算符,它是一个有 open, next, close 方法的 iterator,可以被插到查询执行树中的任何一个或多个位置。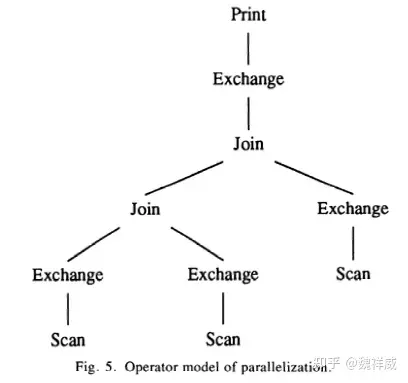
算子间并行(inter-operator parallelism)
Exchange 的 open 方法用于创建进程,Exchange 算子上方作为父进程,下方作为子进程,例如图5中的查询树执行 open 方法后,创建的进程将如图所示。
Exchange 采用生产者消费者模型,父进程会作为消费者,子进程会作为生产者,同时在共享内存中创建一个数据结构 port 用于同步和数据交换。例如 Scan 算子会作为生产者,上方的 Join 算子作为消费者。
生产者端的 exchange 算子会作为 driver 驱动查询执行,其输出会放到 packet 里面。 packet 被填满后,会被放到 port 中,同时发送一个信号量来提醒消费者。
消费者端的 exchange 算子就和普通的迭代器一样,只不过它接收输入时会通过进程间的通信而不是内部的方法调用。
注意,火山模型中所有其他模块都是基于 demand-driven,即 iterator 调用 Next() 方法后,数据流再从下游传到上游,控制流和数据流的方向相反。而 **Exchange 算子则是基于data-driven,生产者侧的数据就绪后再通知消费者执行,数据流和控制流的方向相同。可参见下图的 Pull 模型和 Push 模型的比较,容易理解。这主要有两方面的原因:
- Data-driven 的方式更容易实现算子内的并行,因为算子内并行需要对数据进行分区,然后基于不交叉的数据进行;
- 这种模式避免了多余的控制流来 Request data,进程间通信时这些不避免要的控制流会导致延迟。
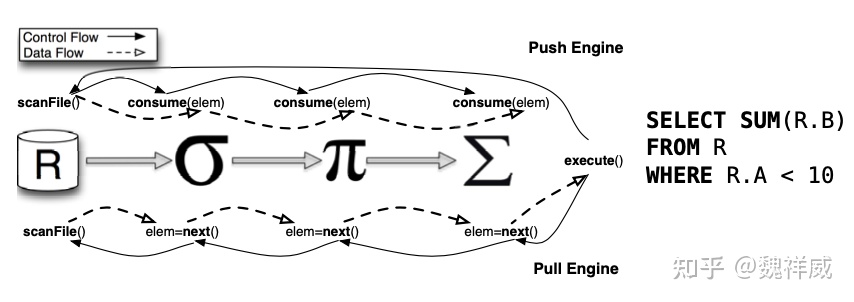
同时,data-driven 的模式下允许流量控制(flow control) 或者说反压(back pressure)。比如说,当生产者的生产速度大于消费者的消费速度时,会导致数据堆积,占用较大内存的问题。这时可以通过消费者端发送一个信号量,告诉生产者降低生产速度或停止生产,等消费者消费完后再进行,从而解决问题。即改用拉取模型和推送模型。
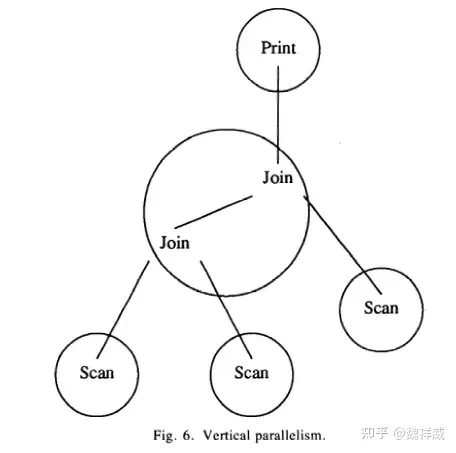
算子内并行(intra-operator parallelism)
算子内的并行需要对输入数据进行分区,输入数据主要包括数据存储和中间结果。
- 数据存储的分区主要依赖物理分区,比如不同设备,不同文件。
- 中间结果分区则主要依靠在 port 中使用不同的队列。生产者使用分区 support function 来决定放到哪个队列里。
图7中展示了为了实现算子内并行创建的进程,Join 算子有三个进程执行,Scan 算子由一个或两个进程执行。通过规定_并发_度(degree of parallelism)来确定执行的进程数。因为同时有三个进程在执行 Join 算子,因此必须对 Scan 得到的数据进行重分区,以交给不同的进程执行。

所有的 Scan 进程都可以传递数据给所有的 Join 进程,但是 Join 算子间的数据传递只允许在每个 Join 进程内部进行。此时,如果使用了基于分区的并行 Join 方法,且图7中两个 Join 是针对不同属性进行的,则会导致出现问题。因为第一个 Join 是用属性 1 做的分区,此时属性2 相同的 tuple 可能落在不同的 Join 进程中。这个问题可以使用 exchange 算子的变式来解决,称为 inter-change.
Exchange 算子的变式
目前,我们提到的 exchange 算子都只能在一个进程的顶部或底部出现(要么提供输入,要么进行输出)。除此之外,Exchange 还可以在一个进程的 operator tree 的中间出现,其功能只限于提供一个数据交换的窗口。其 next 方法从下游的算子中获取输入,并可能把它发送给同一个 Group 的其他进程(如果属于自己的分区就自己用)。这种操作模式称为 inter-change.
另外,还有能把输出广播给所有消费者的 exchange 算子, 比如 HashJoin 中广播小表构建的哈希表;根据 producer 把 input 分别存储的 exchange 算子,以便上游可以区分输入的来源。
参考
Volcano - An Extensible and Parallel Query Evaluation System
Push vs. Pull-Based Loop Fusion in Query Engines
Apache Spark as a Compiler: Joining a Billion Rows per Second on a Laptop
为什么向量化计算(vectorization)会这么快?
PgSQL · 引擎介绍 · 向量化执行引擎简介
SQL 查询优化原理与 Volcano Optimizer 介绍
一篇文章掌握 Sql-On-Hadoop 核心技术
知乎问答-马晓宇-PinCAP
数据库性能之翼:SQL 语句运行时编译
Spark2.0新特性之spark1.x的Volcano Iterator Model(火山迭代器模型)
向量化与编译执行浅析